Once, while I was riding on the A train, I begin observing people sitting across from me. It was a typical NY subway mix. At some point, on the window behind the passengers, I noticed a reflection of the people sitting next to me and of myself. Then the train stopped at the station: The platform was behind me, but I saw its reflection and the people on the platform on the same window across from me, thus adding another, third, layer of images in front of me. Then the door opened and the people from the platform entered the car and stood in front of me.
————-
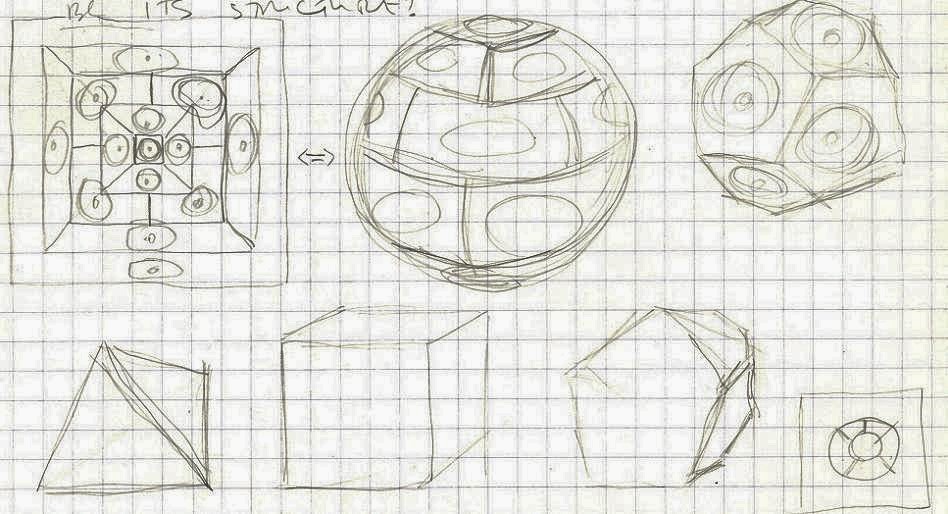
These are random, unsorted notes on time, space, universe, observer, entropy, etc., from my notebook written many years ago (1991-1993), that are now partially presented in this form. Some of the statements are not necessarily consistent, but they show the development of certain ideas. The first several pages are only a visual analysis of some very simple models of the universes defined with 9, 16, and 64 positions and two or three values, based on the 1984 paper by Goran Dordevic Discrete Visual Structures-Elements of Visual Grammar (on this blog).
page 01

p.02
Here J stands for “junction”, the spatial neighboring relationship between different values. The neighborhoods between the same values, “connections”(C) are not marked, but could be calculated by subtracting the number of junctions from the total number of neighborhoods characteristic for a certain spatial structure (9 → 12n, 16 → 24n, 64 → 112n).
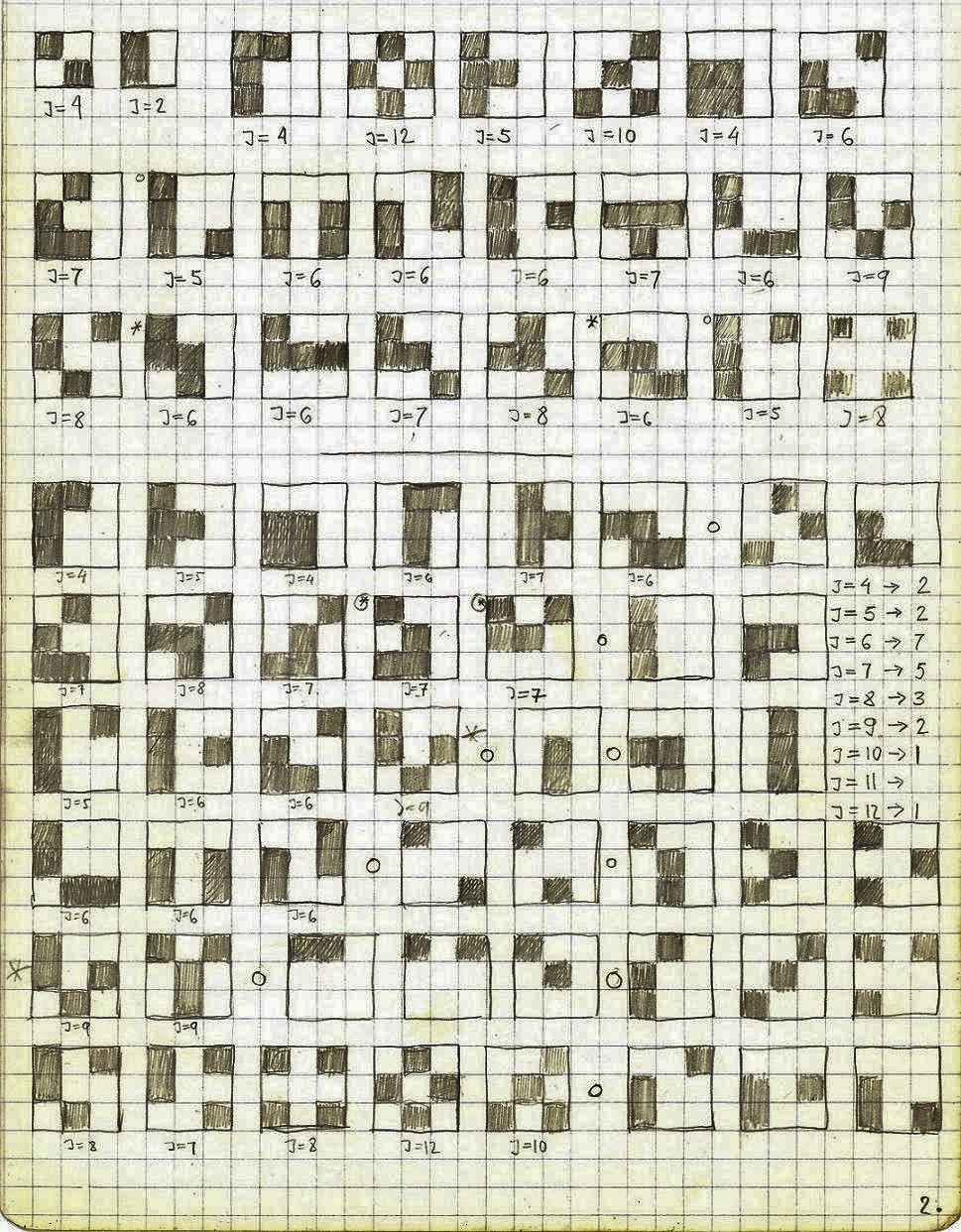
for 3×3 = 9 the number of neighborhoods is 12n → 12:2 = 6 → 9-6 = 3
for 4×4 = 16 the number of neighborhoods is 24n → 24:2 = 12 → 16-12 = 4
for 8×8=64 the number of neighborhoods is 112n → 112:2=56 → 64-56=8
p.03

The number of total spatial neighborhoods for a given matrix type of a square like spatial structure (2×2, 3×3, 4×4, 5×5, 6×6 …) seems could be calculated by subtracting from the total number of elements a number of elements of its one side, and multiply the result by 2.
2×2=4 → 4-2=2 → 2×2=4
3×3=9 → 9-3=6 → 6×2=12
4×4=16 →16-4=12 → 12×2=24
5×5=25 → 25-5=20 → 20×2=40
6×6=36 → 36-6=30 → 30×2=60
7×7=49 → 49-7=42 → 42×2=84
8×8=64 → 64-8=56 → 56×2=112
100×100 → 10000-100=9900 → 9900×2=19800 neighborhoods
p.04

p.05

p.06

p.06b

p.07

p.08

p.09

p.9b
p.10
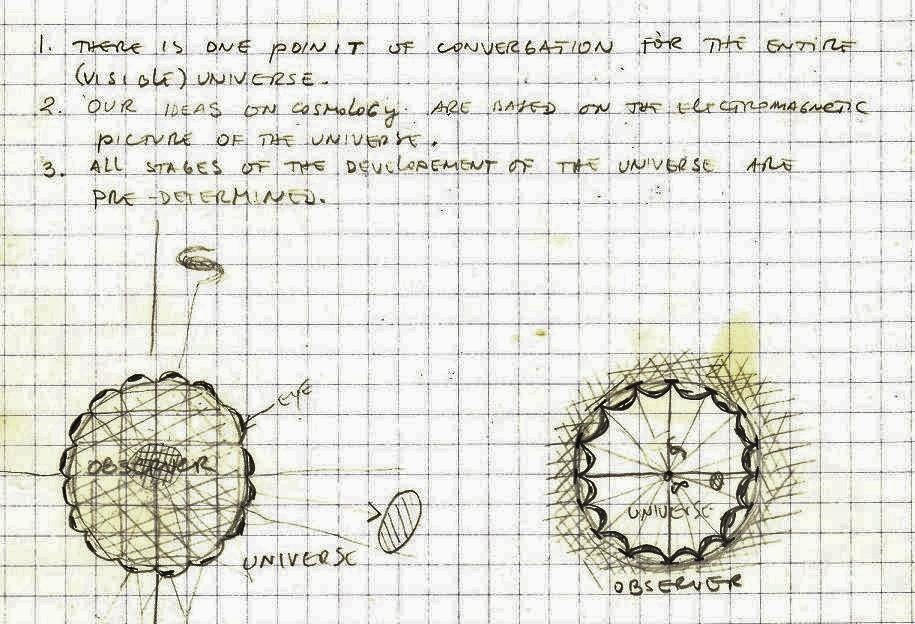
1. There is one point of convergence for the entire universe.
2. Our ideas (knowledge) of cosmology are based on the electromagnetic picture of the universe.
3. It could be that all stages of the development of the universe are predetermined (some kind of the “genetic code” of the universe).
What is the role of a vacuum (a space between light/dark matter) in the question of the open/closed universe?
p.10a
Time is the measure of change. The measure of the “flow” of time is uniform change, which is referential (a clock). It means that the idea of time is fundamentally connected with the notion of change. This means that notions such as “time” and “change” overlap.
p.11
In order to define both time and space there has to be some kind of change (C).
time t = F1(C), distance s = F2(C)
Change could be:
a) a change of position (from point A to point B)
b) a change of state (from hot to cold)
c) a combination of both.
If there is no change (C=0), then it is not possible to define neither distance (space) nor interval (time).
In other words the values for both are zero. C = 0 then t = F1(C) = 0 and s = F2(C) = 0
This would indicate that time and space are derived notions, while change seems to be fundamental.
However, in order for change to be defined there has to be a state of no-change (invariable).
p.12
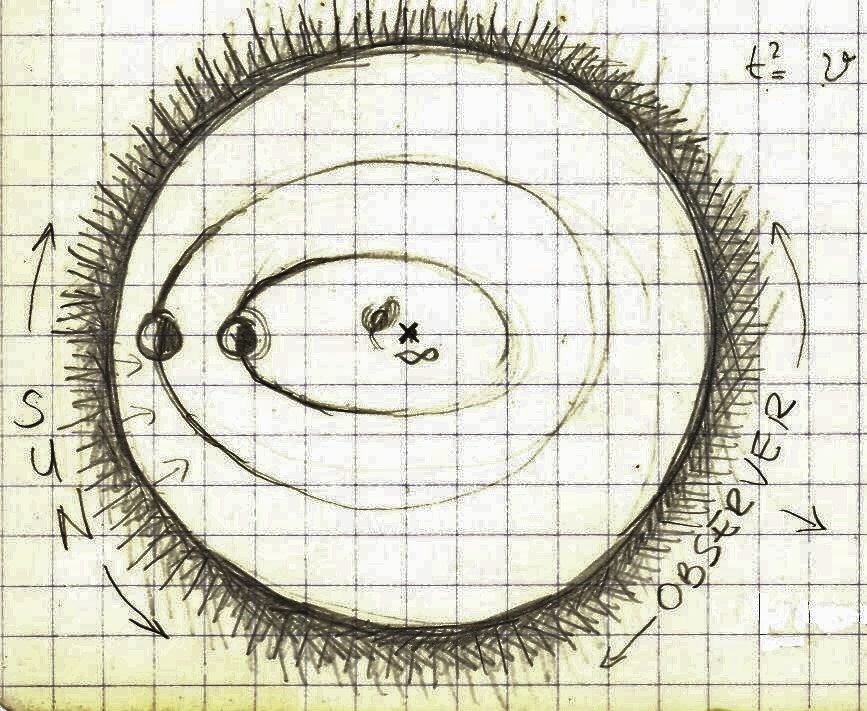
If the universe was expanding slower than the speed of light, then the light (photons) from the Big Bang have passed our solar system a long time ago.
-The idea of a circular time probably has something to do with the repetition of a certain chain of events.
-Perhaps the “red shift” is not correctly interpreted as a consequence of the Doppler effect (galaxies moving away from us). There might be some other explanations for it . For example, how do we know that there is not some kind of vacuum resistance that is manifested only in very long distances? In that case the “red shift” could be explained as a loss of energy of the photon that would cause its wave length to become longer and thus perceived as the “red shift”
(Rv = Kv.s, where Rv is the resistance of the vacuum, s is distance and Kv is some vacuum constant).
p.14
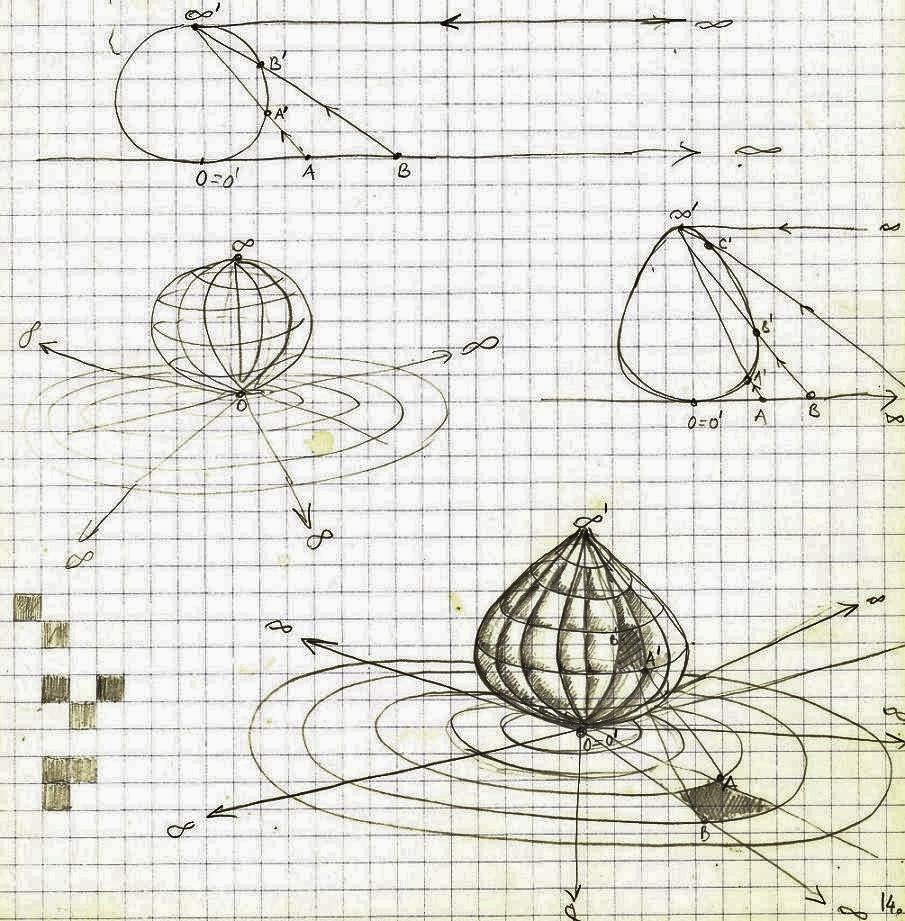
Movement through space could be interpreted not as a change of position but as a transformation of the environment around the moving object – as if the object is still and the environment is moving.
p.15
p.16
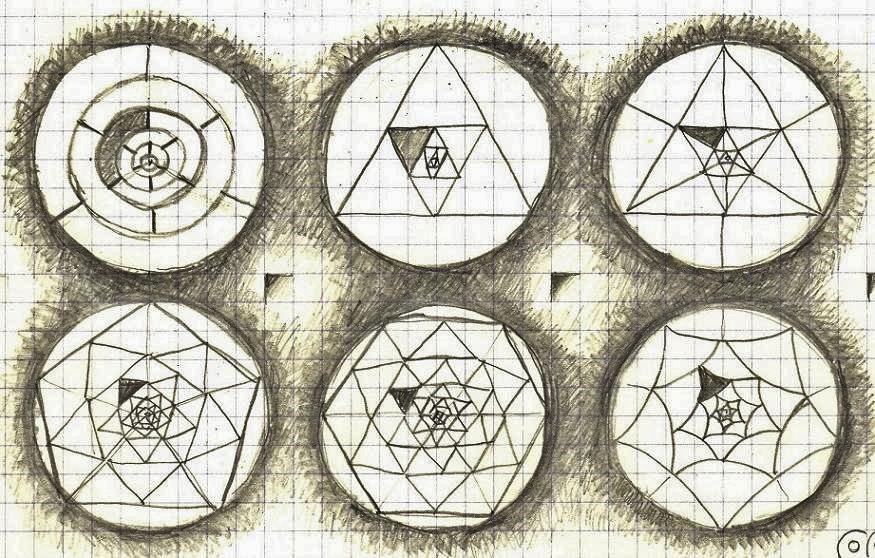
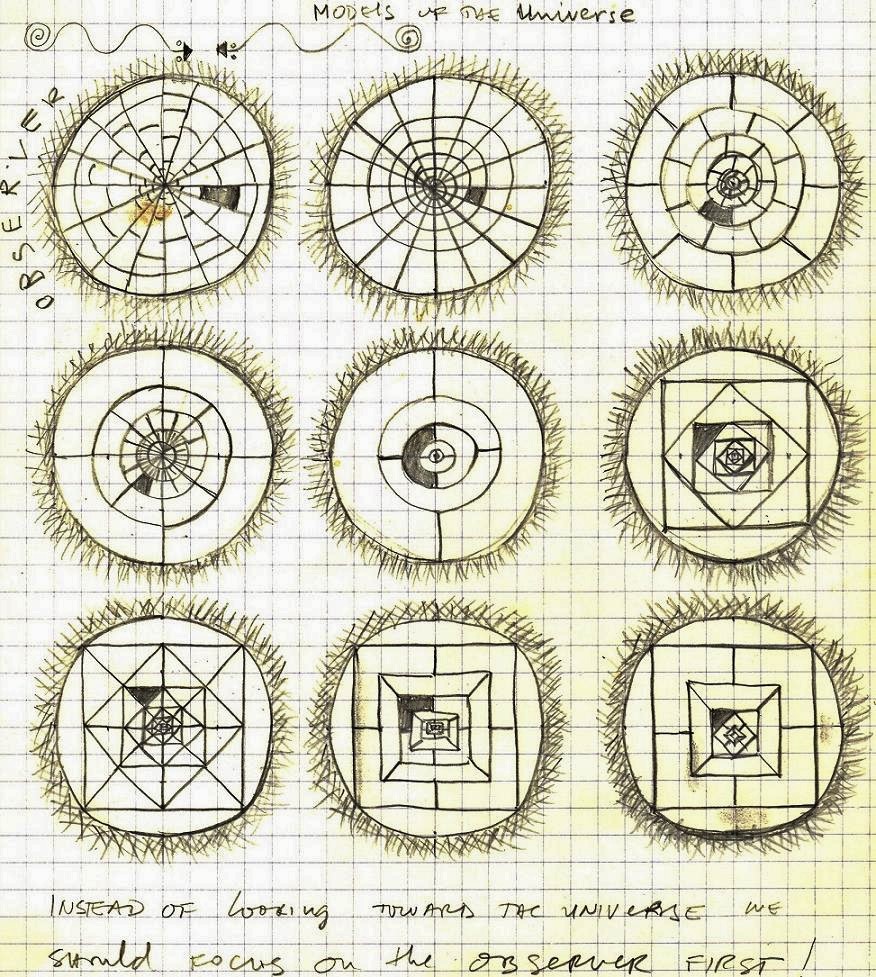
We should consider to what degree the picture of the universe depends on the observer. For example, how does it look to an observer the size of an elementary particle? Or if the observer was as big as a galaxy? How does the universe look like to a blind observer? Or to an observer that lives deep in the ocean?
Or to an observer whose time scale is few orders of magnitude smaller or larger than human (1sec)?
Then we should consider how the properties of the universe itself, its structure, are reflected on the properties of the observer. It is clear that there is a bond between the observer and the universe which is most likely reflected on the compatibility of their structures/properties. The universe is a picture of the observer, but also the observer is a picture of the universe.
p.17
The red shift:
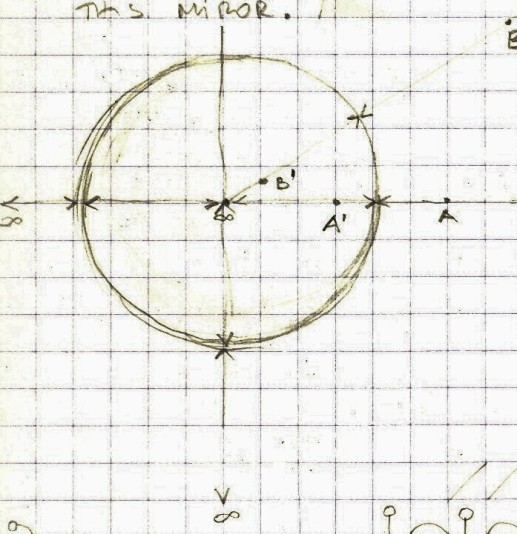
If the objects are moving away from us with accelerating speed, then the “red shift” will change with time as well. If a galaxy is x1 light years away, after some time its distance will be x2 = x + t.dv, since its speed will change from v1 to v2 where (v2 – v1 = dv). In that case the “red shift” at point x2 will be larger than it was at x1. If an object is moving away with constant speed, then the “red shift” will not change with time. In other words, if the “red shift” for a certain object doesn’t change, this would indicate that the object is moving away at a constant speed. If the object is moving away with the accelerating speed, then the “red shift” cannot be constant for that object, it should move further toward the red.

Does any observed galaxy shows the blue-shift, like for example Andromeda that is moving toward us (Milky Way)? And how this relates to the hypothesis of the expanding universe?
p.18
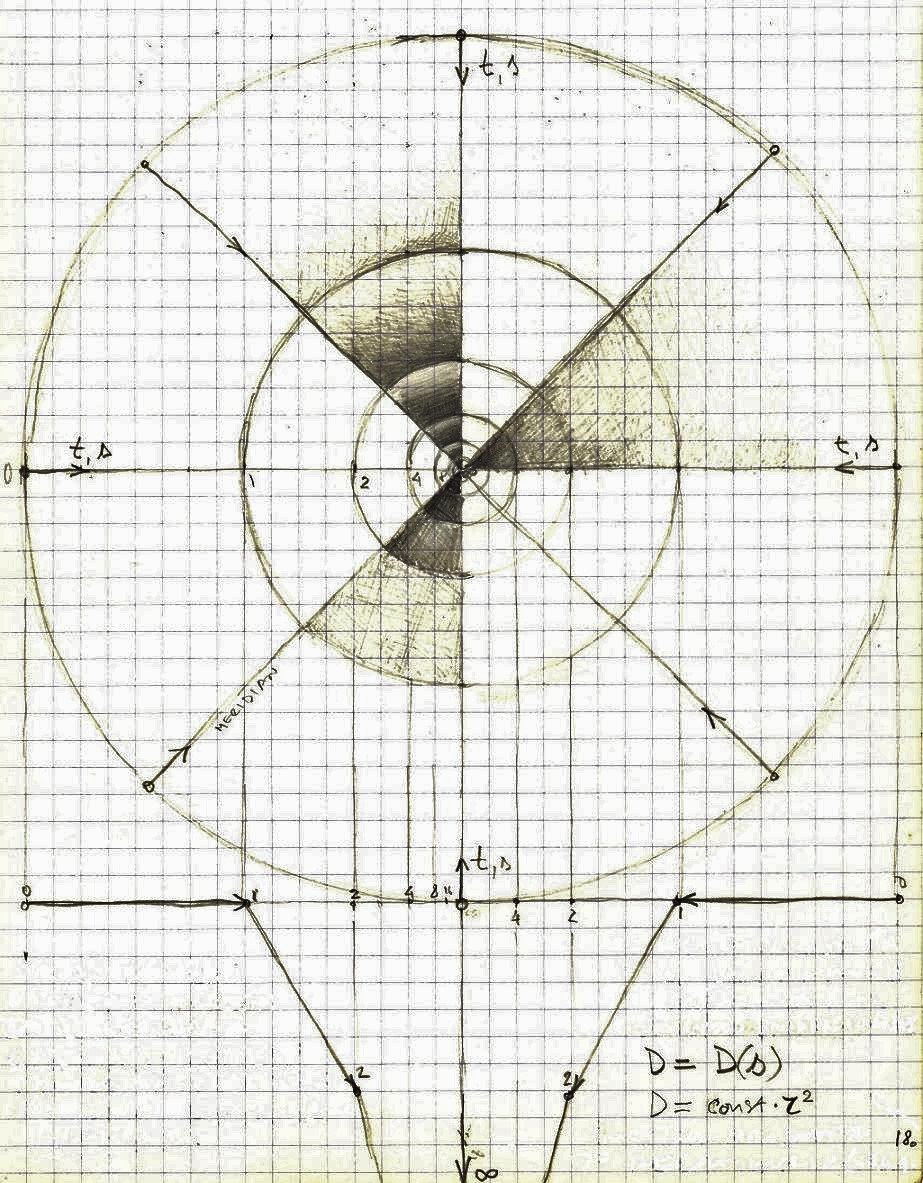
Perhaps we should consider introducing a notion that could be named the “density of space”, and another that could be named the “density of time”.
The density of space would most likely change with distance (the function of distance) in a proportional way: Ds = F(s), let’s say Ds = dc.r2 (where dc is a constant, r – distance). The “density of space” is relative to the position of the observer. Space gets more dense with distance from the observer.
p.19
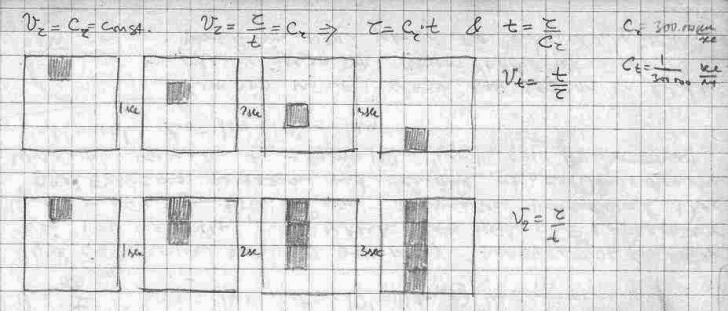
In order to be able to define the “density of space” it would be necessary to introduce a notion of a “spatial unit”, the smallest part of space, some kind of spatial quantum. That would be by definition the smallest and indivisible part (particle) of space. This particle of space is just a position, without any content, but it could be filled with “matter” or “vacuum”. This smallest spatial unit doesn’t change its position, just its content. A motion occurs when a property that occupies a certain spatial unit, leaves it and moves to another. Like for example a series of light bulbs. In t1 only the first bulb is “on”, while all the others are “off”. Then, in t2, the first goes “off” and the second “on”, and in t3 the second bulb is “off” while the third is ”on”…etc. All this would look like as if the “on” bulb is moving from one position to another.
Similarly, in order to define the “density of time” it would be necessary to introduce the notion of the “time unit”. This would be the smallest indivisible time interval, some kind of time quantum.
p.20
In order to get the more complex and more accurate picture of the universe it should be necessary to define different kinds of observers. They could, for example, be different in size. We could imagine observers whose sizes are measured by light years; thousands, even millions of light years.
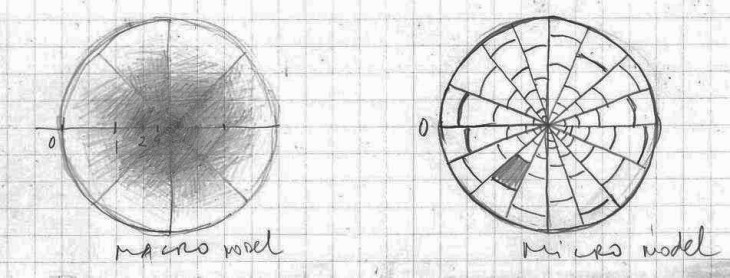
Also, on the other side of the scale, we could imagine observers whose units are one micron, or an angstrom, or a picometer. The limits of the smallest observer are determined by the size of the photon, and the Heisenberg’s uncertainty principle will emerge on some level. One possibility to define an even smaller observer could emerge if there is a much smaller particle than the photon that could be used for observation. At this point it is the size of the photon that determines a meaningful size of the smallest observer (the Lilliputian), while it seems that the speed of light determines the meaningfulness of the largest observer (the Giant). Theoretically, the size of the smallest observer could not be smaller than the smallest spatial unit (spatial quantum).
p.21
It seems that at this point we could identify three limits in the universe/nature:
– the speed of light
– the absolute zero temperature
– the point in infinity (converging center of the universe)
…and perhaps the “black hole” ( if it really exists).
A common property for all these notions is that they, one way or another, represent asymptotic limits. It is not possible to reach them without some kind of fundamental change, but only to approach them asymptotically. Also, there is a certain uncertainty regarding the definition of the opposite notions. What is opposite to the speed of light? That would be an object with no motion. Something that has the speed zero (v=0). But is there anything that is one way or another not moving in relation to some other object? Would it be possible to find an object in the universe with v=0? That would be some kind of an “absolute zero speed”. Also, what is the opposite to the absolute zero temperature? Clearly, some very high temperature, but what is its value? And what is the opposite position in relation to the converging center of the universe? Perhaps here, where I am standing now, is the farthest place from the center. But my position is changing every moment as I write these words.
The speed of light might be important to define how a change is transmitted from one spatial unit to another. In case of the photon, it should be the speed of light. It might be that the speed of light could be useful in defining the “referential time” and “referential space”, in other words the “referential observer”. These would be some kind of fixed notions that would enable defining and measuring changes in the universe.
The question is how to define the smallest spatial and time units and what could their values be?
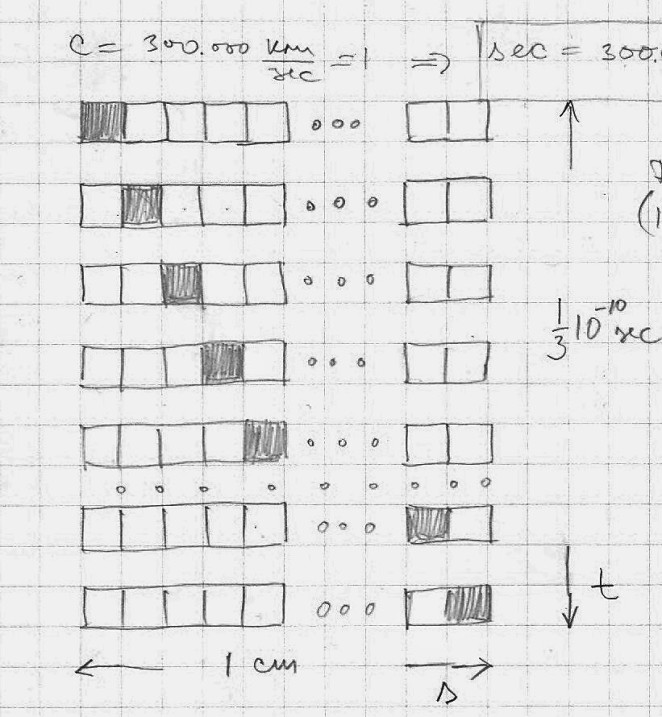
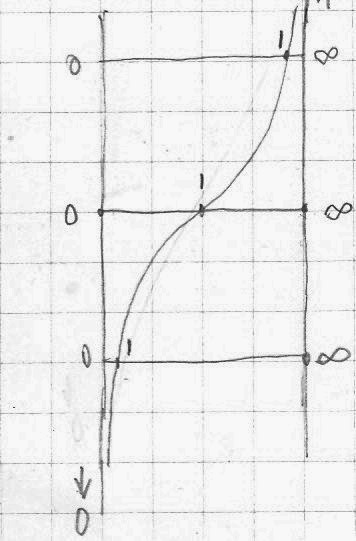
Another thing, we define speed as the change of distance in a time unit (meters per second → v=s/t). However this is in fact the definition of the “spatial speed”, the change of position in a time unit. Would it make sense to define a “time speed”, a change of time with a spatial unit (seconds per meter → y = t/s)?
These notions make sense only when there is relative motion. There is no change of space/position without change in time, and vice versa, there is now change in time without change in position. But what about a change that is not of position but of value, a point that is hot becomes gradually cold?
There is no change of position here but there is change of time. Perhaps we should define two different notions of time: on would be “spatial time”, which is in relation to change of position, and another “value time”, which is in relation to the change of value (state).
p.22
The speed of motion through space is defined as a change of position along a certain trajectory (path) within a time unit/second (v = s/t), while speed of motion through time could be defined as a change on a time trajectory in a spatial unit/meter (y = t/s).
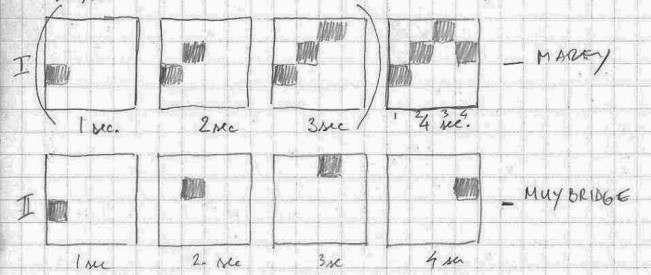
It might be interesting here to compare two different kinds of recording the motion/movement. One was introduced by Etienne-Jules Marey, and the other by Eadward Muybridge. In the case of Marey we have one frame (space) within which positions of a moving body are recorded in different instances of time. Here change is taking place in a function of time within a single space. On the other hand, in the case of Muybridge we have a series of frames (spaces) in which we see a body changing position from one frame to another. Here change is recorded in a function of space.
This also seems to relate to the Heisenberg’s uncertainty principle. In Marey’s case in a single frame
we see the trajectory/direction of the movement that is recorded but we do not know the exact position for each instance since they are blurred by overlapping, while in Muybridge’s case within each frame/space we could clearly define a position of a moving object but in principle we wouldn’t be able tell the direction in which the object is moving.
p.22a

Marey is change that is happening in time within one spatial unit, change is the function of time, while Muybridge is change that is apparent only as a series of different spatial units (frames) in one time unit, change here is in the function of space.
We should here distinguish the actual time and space that are changing during the filming/recording of these movements in both the Marey and Muybridge cases. The times and spaces we are defining here are those of the observation of the recordings (photographs) of the changes, not of the changes themselves.
space speed → v = s/t (m/sec), time speed → y = t/s (sec/m), => y = 1/v
The “time speed” (y) is a movement (change) in which the time taken for an object to move through the spatial unit (meter) is measured, the number of seconds an object needs to pass through 1m. Since the time speed is proportional to time, it is inversely proportional to the space speed. In other words, this means that the slower the object moves through space, its time speed is higher, it needs more time in order to pass through the spatial units. If the object is not moving its time speed is infinite → ∞ (?).
All this sound counter-intuitive but it might make sense in certain situations.
If the (spatial) speed of light is c = 3×108 m/sec, then the time speed of light should be w = 1/c or w = 1/3×108 sec/m. This means that the time speed of light is very slow, while its spatial speed is very high.
p.23
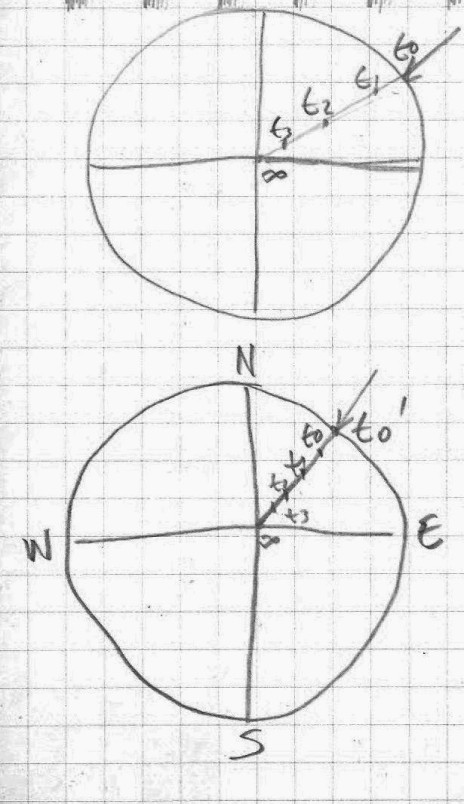
When we are observing the cosmos, or taking a picture in a certain moment, it is like a Marey’s photograph. We see different time layers in a single frame/spatial unit. When we take pictures of the cosmos in several instances, then in a way we have a combination of Marey and Muybridge.
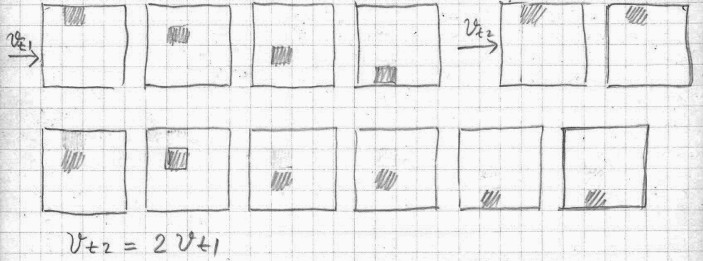
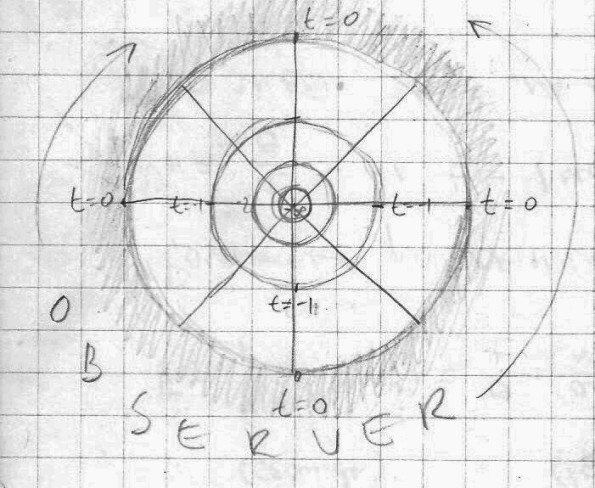
The timeline of separation between the observer and the universe is the present → now.
All the points within the radius t0 → ∞ are in the past. The way t0 in a certain instance becomes t1, in another instance is the way in which the entire universe is moving through time toward the point in infinity (∞).
p.23a
P.23b
p.24
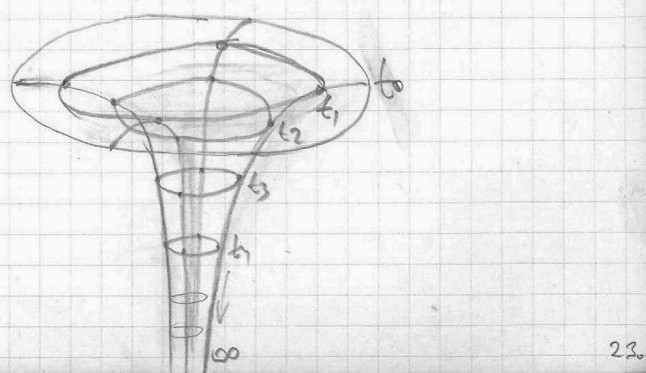
Is it possible to have simultaneity (same time) for two spatially separated events?
And, is it possible to have the same space (spatial identity) for two time-separated events?
Or any event is unique both, regarding its time and space locations.
If we have a clock on the wall, each day it will repeat the “same time”, but although the clock is not moving in relation to the wall, it is not still, it is moving in relation to countless objects in the universe. As we cannot get back to any point in time, we could not get back to any point in space. Because any point in the universe is moving in relation to time (to its previous time mark) and in relation to space (to its previous space mark).
One of the fundamental questions is how to define the relationship between the observer and the observed. Is the observer a part of the observed? Most likely the answer is-yes. It is a kind of binary system in which no part could be defined independently of another (like black-white, hot-cold).
This is why the universe should be defined as a unity/bond and an interaction between the observer and the observed. It is usually assumed that the observer is everything that is not what is being observed. However, if the observer and the observed are united/overlapping to a certain degree, then we have to define a borderline between these two entities/phenomena. Usually we place the observer within the universe, and the observer is observing the universe from within. On the other hand we could imagine an observer that is enveloping the universe and observing it from the outside. In that case the universe is contained within the observer. The physical border between the observer and the observed in terms of time is the present moment(now) and spatially-here. Everything that is observed around is in some kind of past, because of finite speed of light. The further we see the more in the past it is.
The position of the observer being here and now is referential, and everything else is measured in relation to this position. Definition of an observer depends of the character of its interaction with the observed. In our case, these are primarily the electromagnetic waves. How the observed appears to an observer depend of the properties of the observer. How the world could appear to an observer which can not pick up the electromagnetic waves, but could feel heat and hear the sound? In this attempt to define an observer I am appearing in the role of a meta-observer. I am observing both the observer and the observed from some kind of outside position.
The inside of an eye-retina, could be a model for an observer.
p.24b
Time interval (referential)
Let’s say there is a smallest (shortest) time interval so that all other intervals are its integer values. This time interval will be the referential interval. A uniformed series of such intervals along a linear structure is some kind of referential time. Between two neighboring intervals (two time units) there is no any other time interval. We could imagine that the entire universe turning “on” and “off” (appear, disappear, appear, disappear …) in the rhythm of the referential time. And if an observer has a rhythm different from the time unit, it might not be able to observe this. What it will see is a continual series of the pictures of the universe when it is either “on” or it will see nothing if these are the images when the universe is “off”.
Question is if it is really possible that the universe(s) is appearing and disappearing and how to define its generator. In each of these instances the universe(s) are “frozen” without any motion like Zeno or Muybridge.
Entropy is defined as a measure for disorder (or order). Higher disorder → higher entropy. However, entropy might be interpreted as a measure for change. The higher the entropy is within a certain system, the smaller the possibility to distinguish the environment when changing the position from point A to point B. In the state of entropy the state around point A is indistinguishable from the state around any other point (B), and the change cannot be observed.
p.25
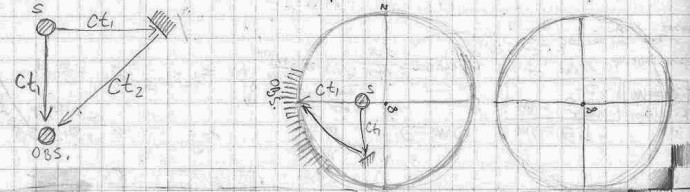
Let’s assume that the light (photon) is moving from one object (A) to another (B) separated by 1 light minute. It is the distance that light passes in one minute.
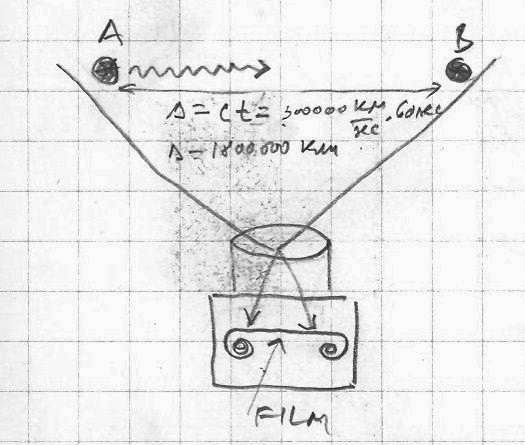
Let’s say also that a movie camera is placed at a certain distance equal from both objects and both objects are within the camera frame and the camera is taking 40 frames in one second (2400 frames in one minute). We are recording (filming) light (photon) that is traveling from object A toward object B at the speed c = 3×108 m/sec. At the end of one minute we will have a recording of the photon traveling from A to B with a speed of light in 2400 frames. If we project this film with its recording at the speed of 40 frames/sec, we’ll observe a photon traveling from A to B in one minute. However, if we instead project the film at 80 frames/sec what would be the speed of the photon? Is it going to be twice as fast (2c)? Or if we project the same film at half the speed (20 frames/sec), would then the speed of the photon be half of the speed of light (½ c)?
All this relates to the question what is the maximum number of frames possible for a camera to record a certain event? Here this question is that of principle, not related to technology. We assume that we have the best camera that has ever been made. This is related to the definition of the smallest time interval. No camera could film faster than that.
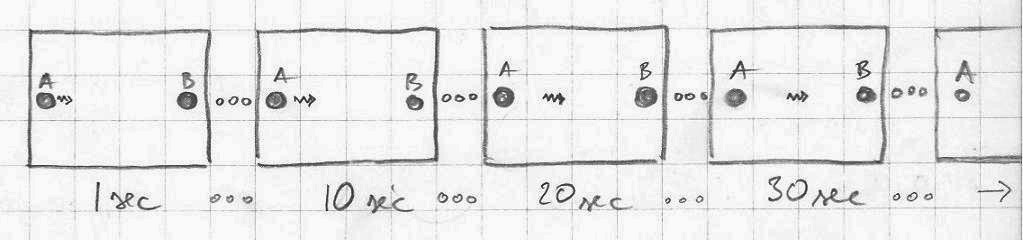
If we could film the entire cosmos in an interval of a billion years, with let’s say a thousand frames per second, and then run the film faster or slower, would then the laws of physics look different?
Then, another interesting question is an observer’s perception of speed. What is the maximum number of “frames” per time unit (frequency) an observer is able to perceive and process? The question becomes more complex if this frequency is not uniform but changes with time.
26.
Then there is the question of the relationship between the size of an observer and its time unit. Can an observer be as big as a galaxy and its time unit to be 1sec? Or should the scale of the observer’s time unit correspond to its size (spatial unit). Let’s say, for a 1m observer the time unit should be 1sec, and for an observer of 100,000 light years in size, the time unit should be perhaps 1000 years.
We could ask ourselves how much this “speeding up” the time or “slowing it down” by varying the speed of the film projection corresponds to some kind of “reality”. How much is this kind of manipulation of recorded natural events telling us about the real world? When we, for example, film the growth of a plant in slow motion (one frame per second) and then project the film at a normal speed (24 frames per second).
In a span of few minutes of our “real” time we could see the dynamic growth of the plant that took place over several days. Or a flying bullet filmed with a high speed camera in one second, and then projected at a normal speed for several minutes. We will see the bullet flying in slow motion and could notice many things that will not be possible to notice with the real time speed.
I could imagine an observer who in relation to my speed of observation (24 frames per second) has a much slower speed, let’s say only one frame per second, but who in his own time perceives this as a normal speed. Would then for that observer the speed of light be 3×108 m/sec? I would say no.
In this case the speed of light might still be constant but not 3×108 m/sec.
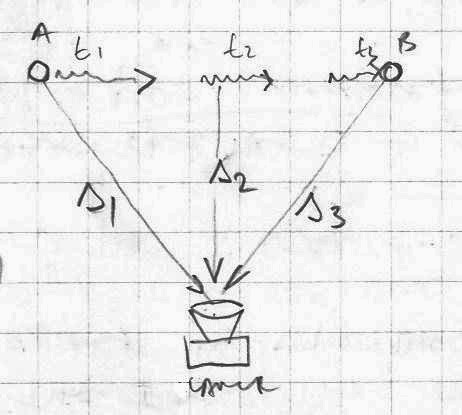
Let’s consider this case: We are again filming the traveling of light (photons) from object A to object B with a camera fixed in relation to both objects and with both objects visible within the camera frame.
Let’s say that the speed of recording (filming) is 240 frames per second (10 times higher than normal).
For a photon to travel the distance of 1 light minute the entire recorded event would last 1min real (my) time. If we now project this film at a normal speed of 24 frames/sec the projection will last ten times longer (10minutes) and the photons should thus travel 10 times slower: 1/10 of the speed of light.
However, if we now project the same film at a changing speed, starting with 24 frames per second and gradually speeding up so that in the middle of the film it is 240 frames/sec while toward the end the speed becomes 480 frames per second, what will be the speed of light be in these three instances? Logically in the beginning it should be 1/10 of c, in the middle 1c and toward the end 2c speeding up gradually between these markers.
Naturally, in this case my time and my observation speed (24 frames/sec) are referential. The speed of light is a reflection of the nature of light itself, but also of the observer as well.
In this case we didn’t consider the fact that light traveling along the straight line from A to B, is not equidistant from the camera all the time. It varies along the trajectory line, being farthest at points A and B and closest to the camera in the middle of the trajectory, half way from A and B. Thus the photons that are recorded by the camera are traveling longer toward the camera from points A and B than from the middle of the trajectory. It becomes even more confusing if we start thinking about what is actually being recorded by the camera, since light doesn’t travel only from A to B but toward the camera as well, which is also 1 light minute away from A and from B. There is inevitably a 1 minute time delay because of the long distances between these three objects (A, B and camera) that has to be taken into consideration.
And furthermore, how is a photon traveling from A to B also sending photons (?) toward the camera and thus being recorded? It is clear that when we define an observer we have to take into consideration all the properties and limitations of the medium that caries the information (light) and the techniques that are recording them (camera). I could only assume how light was behaving on its way before – does it change and in what way?
p.27
Since in essence it is me who is the only “real” observer, all these other cases are invented as some kind of pseudo-observers (for now we’ll leave out earlier mentioned meta-observer). In this way, my time, my size, my properties and limitations in a way how I interact and record are referential. Pseudo-observers are various means to observe the world and improve my interaction with the environment (universe).
In the previous example of filming light while traveling from A to B, we could, for example, place a clock inside the film frame so that the camera could record it as well. Thus the clock will record the speed of the camera as well. When the film is later projected at different speeds, this will be noticed on the clock which will also tick at different speeds (slower or faster than normal). However, I, as an observer who is watching the projection, have my own time independent of the clock. We could imagine a “real” (human-like) observer instead of the camera, watching light that travels from A to B, and its speed of observation to be different from mine. It is quite clear that the speed of light is constant 3×108m/sec. in some referential systems, like ours, where we measure distance in meters and time in seconds the way they are defined. But, is the speed of light constant and the same in all referential systems we could imagine? What if a referential system is not linear in relation to ours?
What if an observer is on the photon, and travels with it, what would be the speed of light in relation to this observer?
We should think carefully about this introduction of the camera (and film) as a pseudo-observer, and if it has some deeper meaning and not as a superficial idea (a camera as an eye and a film as a memory). Since not only could we project the film in different speeds, but we could also run it in reverse, the question is: to what degree could what we see in the reverse projection be useful in interpreting the “real” physical phenomena, whatever “real” means. It definitely relates to the properties of the (referential) observer, its means of perception and processing outside information, memory, consciousness and the limited duration of its existence and its end. How much the observed plays a role in the end of the existence of the observer?
p.26b & p.27b
“- Einstein’s theory of gravity, known as the General Theory of Relativity, is one peg.
– The fact that the universe expands – that intergalactic space is stretching, carrying vast clusters of galaxies apart from one another at velocities directly proportional to the distance separating them, is another sturdy peg.”
– Is there such thing as a “genetic code” of the universe that determines the way it develops?
– If the Big Bang is true, then we are at any given moment on the time (and space) front-line in relation to the beginning of the universe. We are, “here” and “now”, at the farthest point from the “beginning of the universe”, if it really happened. Everywhere we look around, we see the past, recent or distant, and all the observed objects are “younger” in relation to the ever present moment here where I am standing. It seems there is no simultaneity between different spatial positions possible.
– The definition of the relationship between the observer and the observed is fundamental. It would not be possible to define the observed without an observer and vice versa.
– If the observer and the observed define each other, are they overlapping and to what degree? Where does the observer end and the observed begin? However, there must be a part of the observer that is not part of the observed, and there is part of the observed that can never be reached by the observer.
– Could the relationship observer-observed be self-reflexive, when the observer is observing itself (self-observation) and how can it be defined, and is there a part of the observer that cannot be reached by self-observation?
– What does it mean that the space-speed of a certain object is v = 0 (s = 0)or that the time-speed of an object is y = 0 (t = 0)? Does this have something to do with the Heisenberg’s uncertainty principle?
Muybridge → position known (momentum unknown)
Marey → momentum known (position unknown)
In each picture of a Muybridge’s series we could precisely determine the position of an object but not the direction in which it is moving. On a single Marey’ picture we see a series of positions of an object that will show the trajectory (direction) of the moving object but we would not be able to determine precisely its position when looking at the picture.
Muybridge picture is change observed through a series of spatial units in simultaneously, while Marey’s picture shows a change through a series of time instances in a single spatial unit(picture).
– There is clearly a connection between Muybridge and Zeno’s arrow.
– It could be that any motion is irreversible. This would implicate that not only is the “flow of time” irreversible but the “flow of space” as well. If two spatial points are standing still in relation to each other, it would correspond to two synchronized clocks. From the position of each clock there is no change on the other. Both time and space are symmetrical toward each other, since both notions are derived from a more general/fundamental notion that is change.
-We should also take a closer look at the relationship between wavelength (space) and frequency (time).
p.28
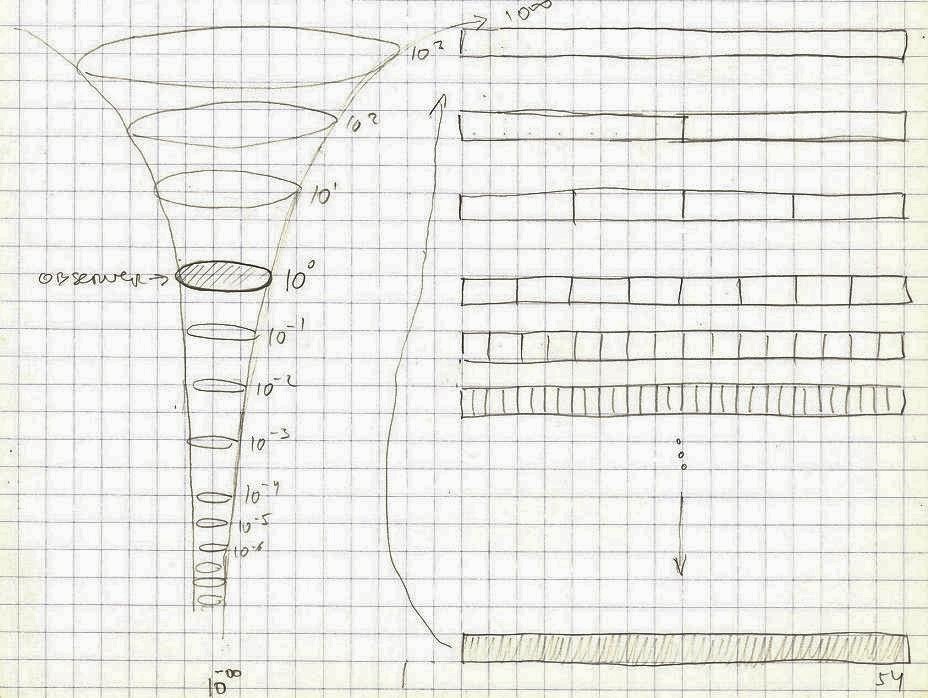
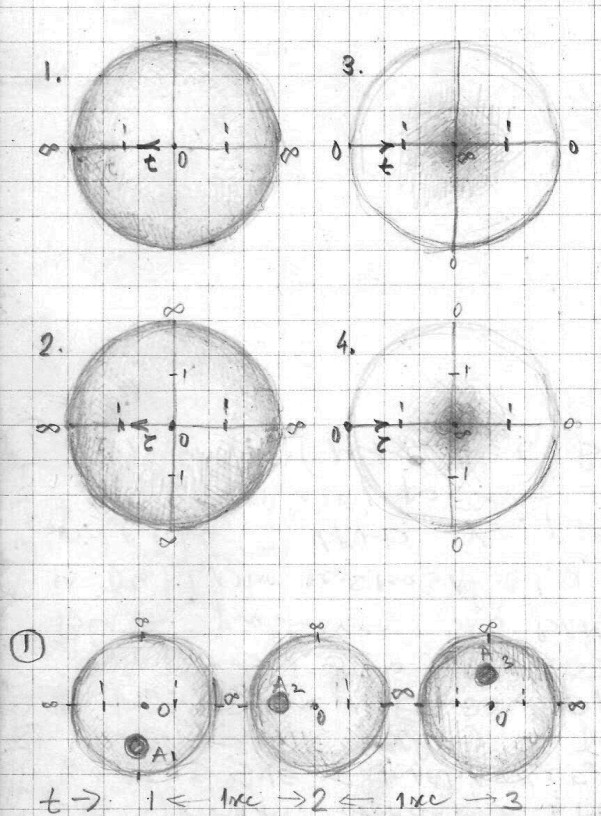
We should now say something about a model which for the observer has a convex spherical mirror (SM) whose diameter is 300,000 km (one light second). If this spherical mirror is placed somewhere in space not very far from the solar system (30 light days away) from where the Sun would be just a very bright star but the cosmos looks not very different as seen from the Earth, we could assume that the entire visible cosmos will be reflected in that mirror. Closer objects, like our Sun would appear closer to the mirror’s surface while distant objects (stars, galaxies) would appear to converge toward the geometric center of the mirror. This mirror would represent a pseudo-observer while the “picture” of the cosmos reflected on it is one possible interpretation (model) of the cosmos. In this case only the space inside the physical sphere is not reflected and remains unobservable.
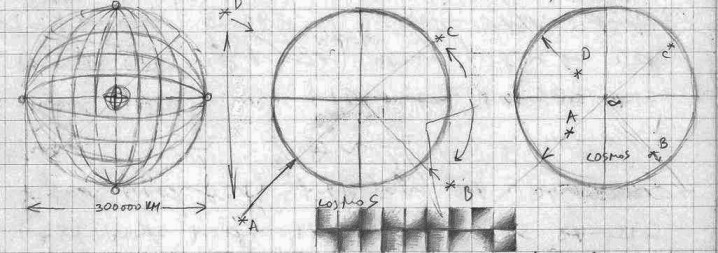
We could now imagine that this is not just a picture but that is how actually cosmos looks like, that its spatial structure is converging toward a single point in the center which can be approached only asymptotically but never reached (like absolute zero, or speed of light). If this cosmos is enveloped with a concave mirror of the same size, the reflection in that mirror will look like the cosmos as we perceive it now. In this concave picture closer objects will appear closer to the mirror surface while distant objects will be spreading in all directions, and the single converging point in the center will be reflected into infinite number of points in the infinity that can never be reached.
If we imagine a spherical surface to be the border that divides space in two parts (interior and exterior),
then any point of the exterior has its corresponding point inside the interior of the sphere, with all the points of the exterior that are in infinity are projected in the one point in the interior which is the geometric center of the sphere.
p.29
An observer could be the “real observer” if what he is observing is outside of it, on the “periphery” of the observed. In the present interpretation, the observer is placed in the center of the observed, and the space stretches from the observer in all directions ad infinitum. In this way the observed “contains” the observer.
Now, if we invert the entire constellation, the observer will appear outside of the observed, but at the same time it is containing (enveloping) it. The observed is inside the observer.
It seems it is not possible to imagine the infinite universe, since its observer will always be one of its limits. Any kind of (observed) universe will have at least one of its limits. And in the case of spherical mirrors, there is another limit: a point in the center that is converging toward infinity in the case of the convex mirror and endless points in the periphery also stretching toward infinity in the case of the concave mirror. These seem to both be viable models. In one, widely accepted today, the observer is in the center and the entire universe is around him stretching toward endless points toward infinity. In the other model introduced here the observer is outside of the universe enveloping it completely, and the universe is structurally converging toward a single point at the geometric center but could never reach it. It can only approach it asymptotically. Then we have these relations:
Observer (center) → Universe (around) → Infinity (diverging)
Observer (periphery) → Universe (inside) → Infinity (converging)
These two models are related to space, but we could imagine two more that are related to time. In that case time will also have structural properties like space: it could stretch and converge.
– The change in size of the spatial element is inversely proportional to the distance from the observer (it could be something like in the law of gravity). Thus, space will have a different “density” depending on its distance from the observer (same thing for time).
p.28b&29b
– Dimensions that differ by order of magnitude 10-10m , 100 m, and 1010m represent in fact different kinds of space, with very different properties. The very definition of the spatial speed depends of the order of magnitude. The notion of space on the 10-10m level should be treated differently from “ours” 100 m. The changing of scale (orders of magnitude) is in itself some kind of movement through space.
– An observer that is 1010 m large, would need some kind of microscope to see the Earth.
– The fact that the force of gravity is inversely proportional to the square of the distance might have something to do that the objects are becoming smaller with the distance, because of the nature of space.
If the the object is getting smaller with distance, than its mass is becoming smaller as well.
This might be an “explanation” for the law of gravity.
– It seems there is a fundamental contradiction between the images of the expanding universe and of the Big Bang. If the universe (space) expands in all directions, then the concentration of matter (galaxies) should decline with distance. However, the further we look the younger the universe that we see. According to the Big Bang the younger the universe is, the smaller it is, therefore the concentration of matter (stars, galaxies) should be higher. These two images seem to be contradictory.
p.30
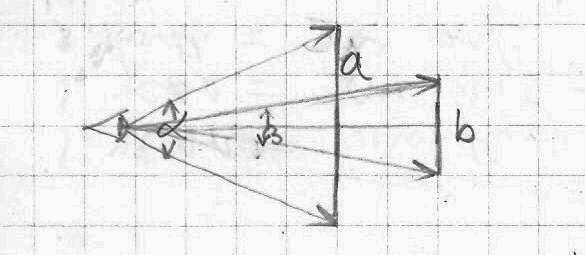
If the distance between the observer and an observed object is changing, then the size of the object is changing in relation to the observer. If the distance is not changing then the size of the object is constant. The reverse might be true, that changes of the size of the observed object indicate a change in its distance from the observer (assuming there is no mechanical change happening, like ice melting).
p.30a
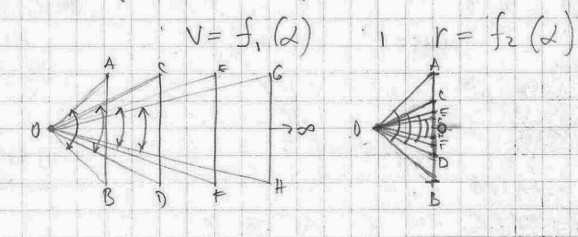
We should consider that the observer is fixed (not moving) and everything else is still or moving in relation to the observer. The size of an object and its distance in relation to the observer could be interpreted as a function of an angle under which observer sees the object.
We will also assume that, not only the position, but the size of the observer to be referential.
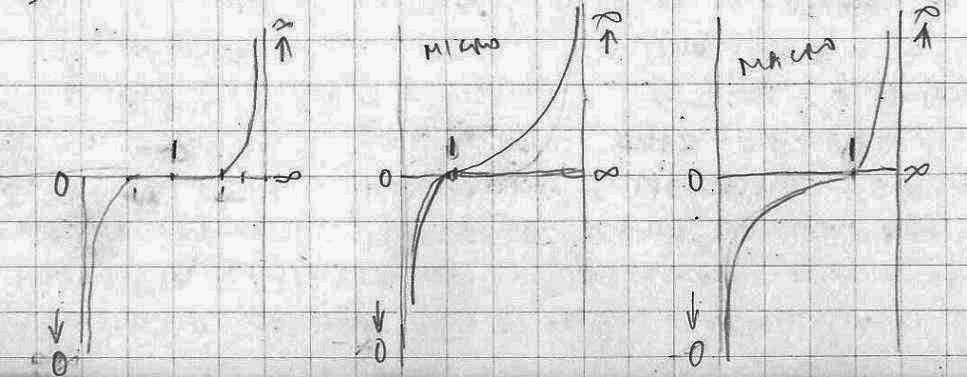
In case of the human scale of an observer we could place it in the middle of the scale (that is position 1) between zero (0) and infinity (∞). The larger the observer is (in relation to a human), the closer is its position to infinity (macro universe). The smaller the observer is, the closer its position is to zero (micro universe).
p.31
If we assume that change is the fundamental notion (together with no-change), then these are three derived notions:
– The change we call time (interval) – measure is “second”
– The change we call space (length) – measure is “meter”
– The change we call magnitude (order of magnitude) – measure is “degree”
It is necessary to define the absolute referential observer that will be standard for all systems and scales. It would correspond to the properties of a human observer. An absolute referential time interval would be 100 seconds, an absolute referential length is 100 m meters, and an absolute referential order of magnitude is 10.
p.31b
The time position of the observer in relation to the universe is always “now” (t = 0) and any other position in relation to the observer is “earlier” (“younger”), it is always before, because of the speed of light. But all this make sense in relation to the electromagnetic nature of the picture of the universe.
Perhaps there is some absolute “now” throughout the entire universe and for all orders of magnitude.
p.31c
p.32
Regarding the definition of the observer we have these four possibilities in relation to the macro universe:
Observer → center, infinity → periphery, time → primary, space → derived
Observer → center, infinity → periphery, space → primary, time → derived
Observer → periphery, infinity → center, time → primary, space → derived
Observer → periphery, infinity → center, space → primary, time → derived
p.32a
p.32b
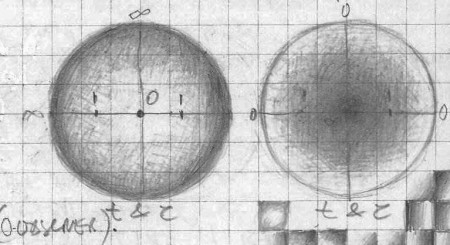
However both time and space, regardless if they are primary or derived (from each other) are a function of change that we assume to be the fundamental notion.
p.33
The fact that the decline in intensity of both the gravitational and the electric field is inversely proportional to the square of the distance, might not have much to do with the nature of those forces, but with the nature of space itself: that objects are getting smaller inversely proportional to the square of the distance.
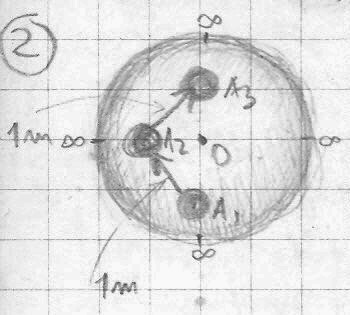
If at the distance of 1m from the observer, an object is 1m high, what would be its height at 2m distance?
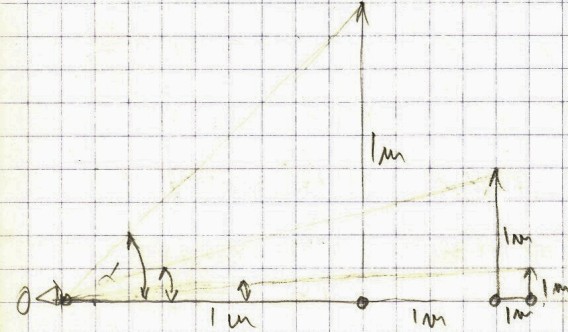
According to this assumption it should be ¼ m. The question here is how to measure the distance if the measuring stick (1m) itself is getting smaller with distance?
Perhaps one solution would be to introduce a standard and unchangeable (rigid) measure unit for both space and time attached to the observer, and these standards would determine the properties of the universe. In some way we have to find (define) a position that is outside of the universe but also outside of the observer. Something analogous to the Cartesian coordinate system. From this referential position and standards we would measure the properties of both the universe and the observer who looking at it. This is why we need to define the absolute referential observer.
Change is generating time, space and magnitude. Magnitude is a property that is applicable to both space and time.
P34.
The important questions are:
– The observer-observed relationship,
– The definition of a standard (referential) observer,
– The rate of converging of space and time.
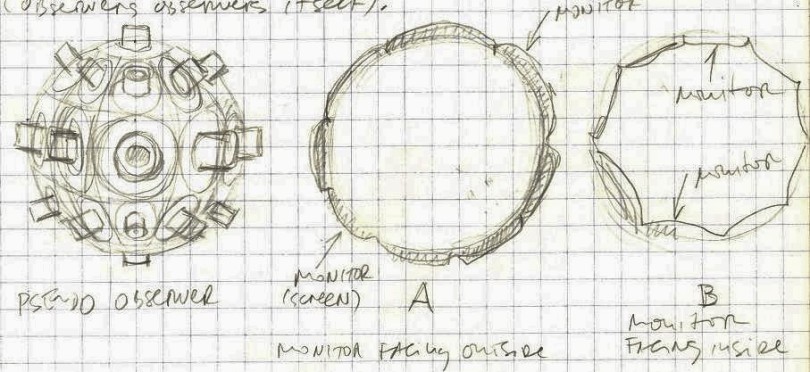
It seems we have to accept that the observer and the observed (universe) are one entity. There is no observer without the observed and vice versa. However, we also have to accept that it is possible to define a clear line of separation (or belt) between the observer and the observed. In other words there is at least one part of the observer that is not and cannot be part of the observed. This brings up a question if the observer could observe himself (self-observation)?
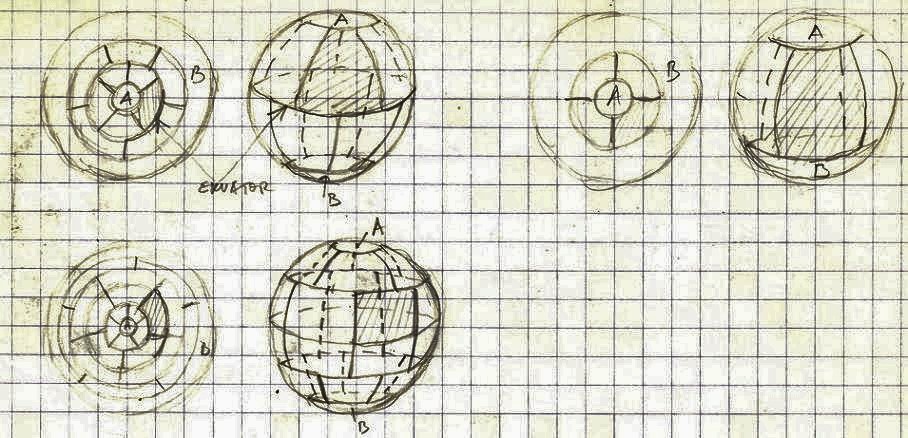
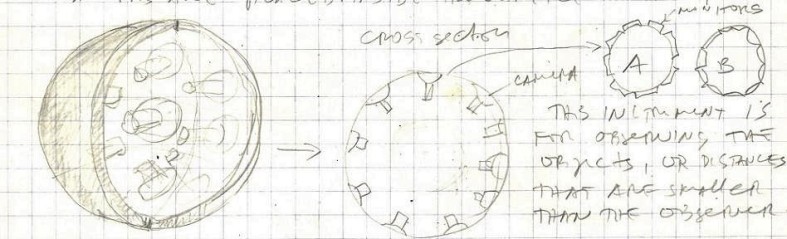
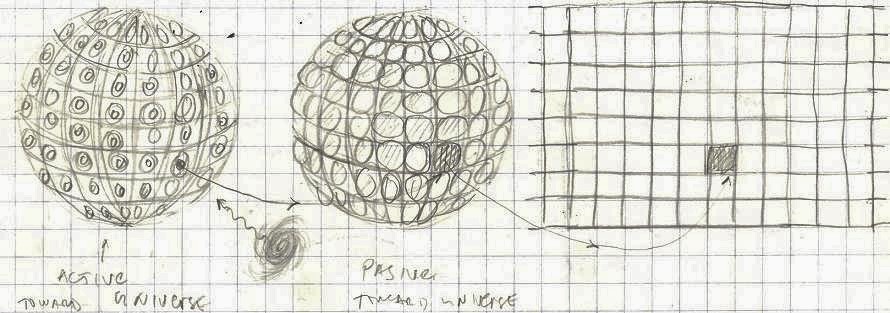
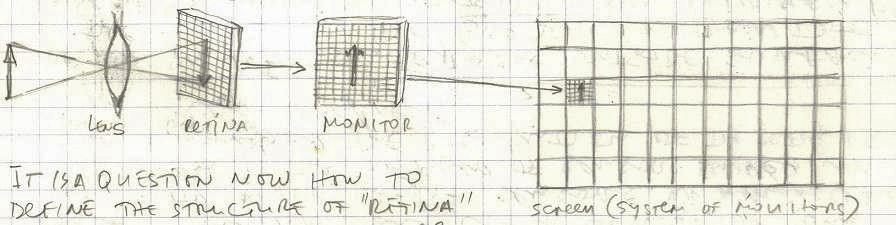
Instead of a spherical mirror as a pseudo-observer we could construct a spherical observer (Pol) with its outside (convex) surface covered with many cameras directing outwards (like the eyes of Argos). These cameras could be connected to the corresponding monitors that are covering the outer surface of another sphere (A) and/or to the monitors covering the inside of a third sphere B. The position of a camera on the Po sphere is the same as the positions of the corresponding monitors on both A and B spheres. This configuration is intended for observing objects larger than the pseudo-observer. The cameras could be equipped with the telescopic lenses for observing distant objects.
If we place Pol somewhere in space and watch on the monitors that we could place on Earth, on sphere A we would see the converging universe, while inside sphere B we would see the diverging universe. Weather they are both static or dynamic is another question.
p.34a
p.35
We could also construct a configuration for observing objects smaller than the pseudo-observer (Pos).
Here cameras are placed all over the interior (concave) surface of the sphere directed inwards. The cameras of this observer could be also connected to the corresponding monitors on spheres A and B.
The lenses of the cameras could be enhanced with the microscopes. In this configuration the micro-world would appear converging on sphere A, while diverging on the monitors of sphere B.
In fact, we could construct a configuration of only two spheres for observing both macro and micro spaces/objects. On one sphere we would install cameras on both its exterior (convex) surface and its interior (concave) surface. On the receiving sphere we would cover both of its surfaces (exterior and interior) with monitors. Each monitor would be connected with two cameras on with macro and and/or with micro lenses. We could switch the cameras depending on whether we are observing the macro or micro phenomena.
p.35a
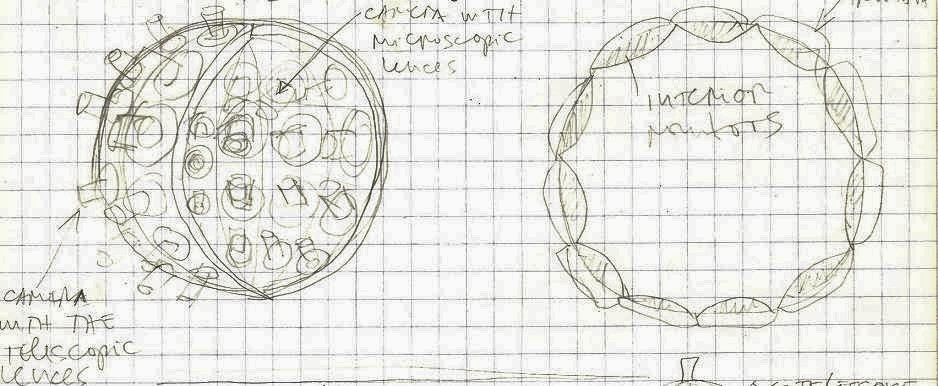
p.35b
p.36
Here we have a sphere with multiple cameras connected with corresponding monitors (on the sphere) that are then all “translated” to a 2D flat screen (according to Rimman’s projection). We need a conversion of the sphere surface into a flat screen since we can not see a sphere from all sides simultaneously.
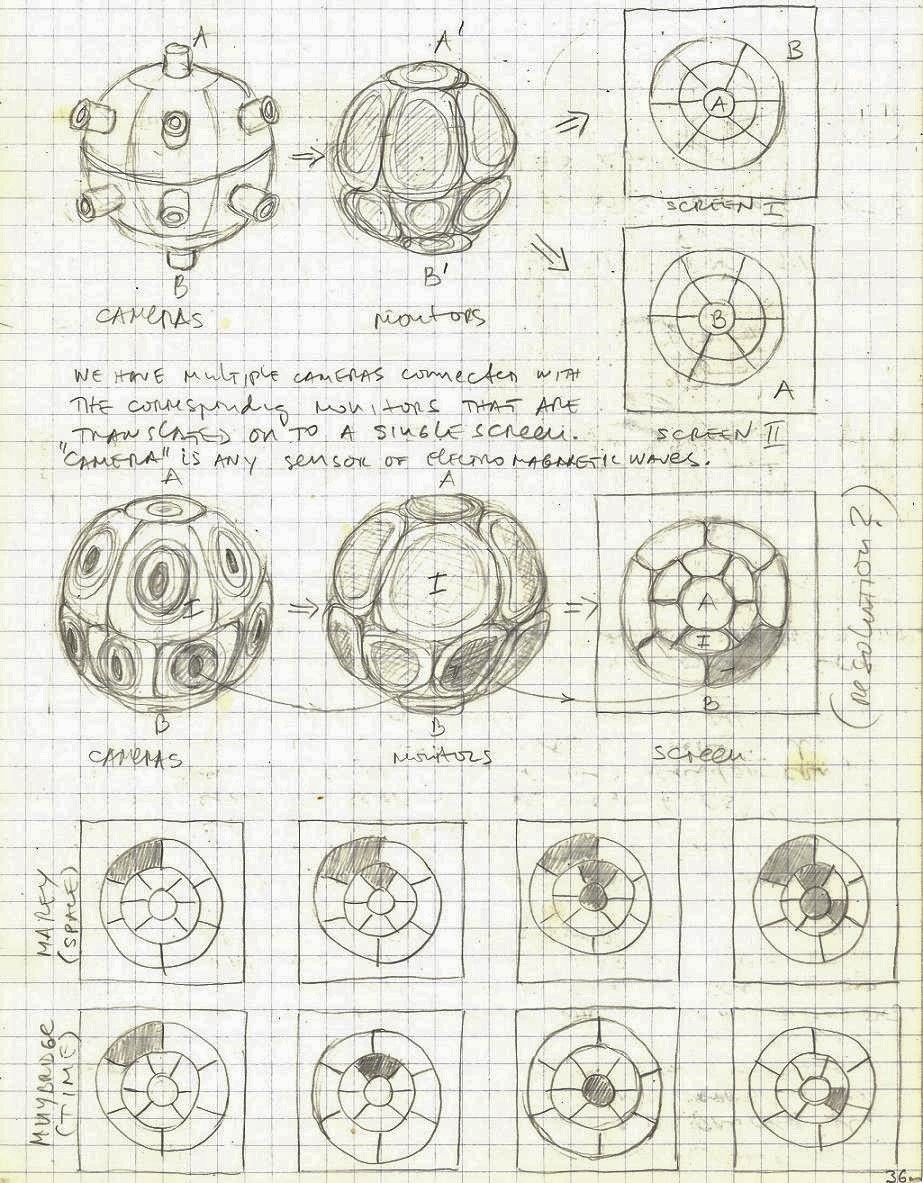
p.36b
Our visual system is based on two frontal eyes and according to this our brain is built to process visual information. The brain is not capable to synthesize inputs coming from more than two eyes. How would the brain of a multi-eyed observer process information? (maybe we wont be able to find out). With the help of the telescopic and microscopic lenses we can (virtually) change the size of the universe (or “change” our size as observers) by orders of magnitude.
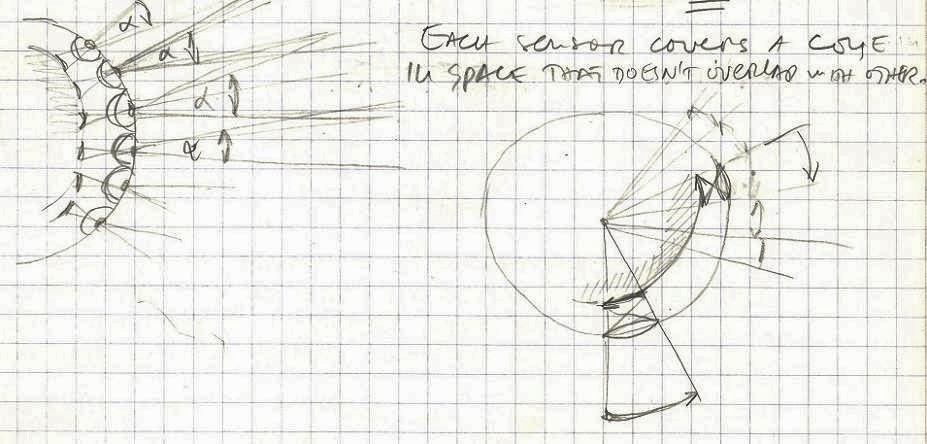
– Then we have to define how many visual sensors (eyes) the standard observer should have
– What kind of (electromagnetic) sensors are these “eyes”?
– The way these “eyes” cover the surface of the sphere (pattern)?
– These sensors should enable observer to see in all directions.
-Each sensor covers a cone in space that doesn’t overlap with its neighbors.
p.37
In order to defining the standard (electromagnetic) observer, we have to determine:
1. The size of the observer (100 m – radius)
2. Time beat of the observer (100 sec – interval/pulse)
3. Spatial resolution – the smallest spatial unit that can be seen/observed
4. Time resolution – the smallest time unit between two inputs.
5. The spectrum of the electromagnetic waves (infrared – gamma rays)
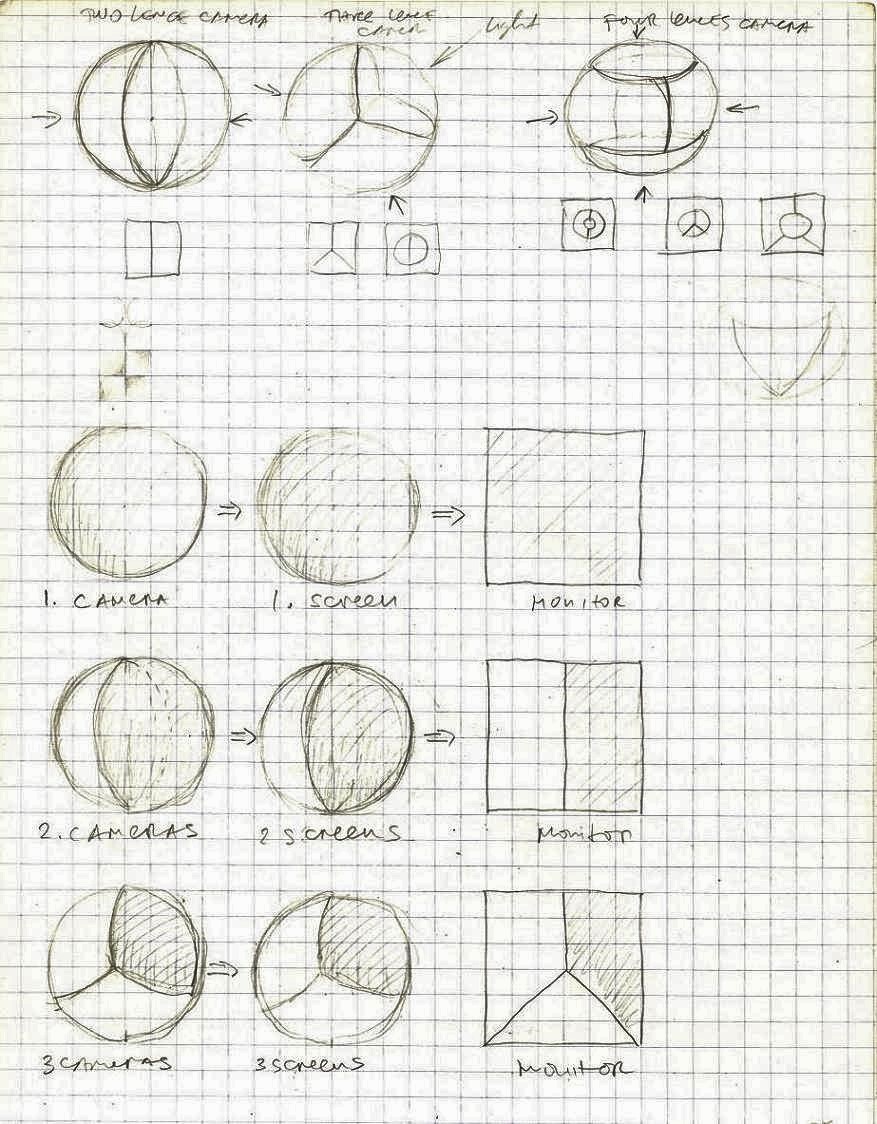
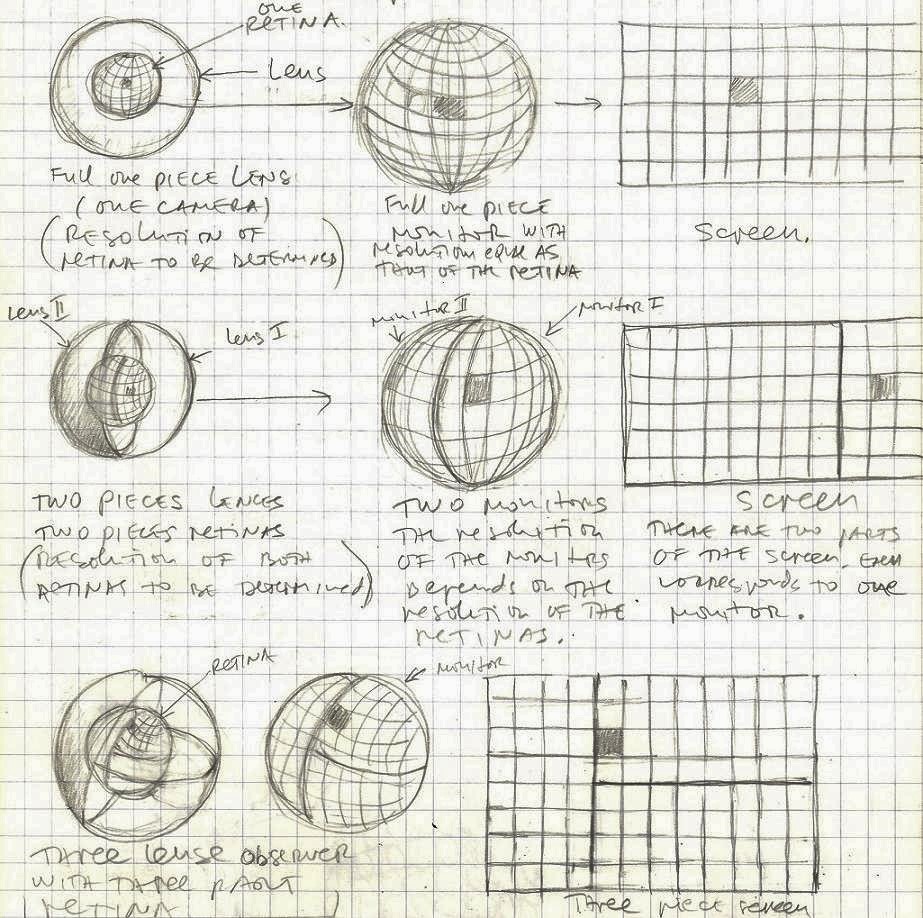
The standard observer (So) should have characteristics as close to human as possible. However, there are some basic differences. First the So can see/detect only electromagnetic waves (not sound, touch, smell or taste). This So will not be able to actually see. It is a complex system/configuration of: a camera on a sphere → a monitor on a sphere → a 2D flat screen. The difference between the “monitor” and the “screen” is that there could be more than one monitor, depending of the number of cameras. Each camera is connected to a single (corresponding) monitor. Then the images of all the monitors are transferred to a single flat screen. There could be different screens for the same camera-monitor configuration, but while the monitor shows a single segment, the screen shows the whole picture on a 2D surface.
p.37b
The interpretation of the image on the screen is basically done by a human (or by some specialized computer, but it too in the final instance has to be interpreted by a human).
The sphere with the cameras could be separated from the rest of the configuration and sent as a probe far away, as some kind of a “remote eye”, while the monitors and the screen remain near us. In some way this is already happening with the Hubble telescope.
We should select one particular (absolute) standard observer to be referential regarding all its properties. This observer is motionless and has uniform beat (time).
p.38
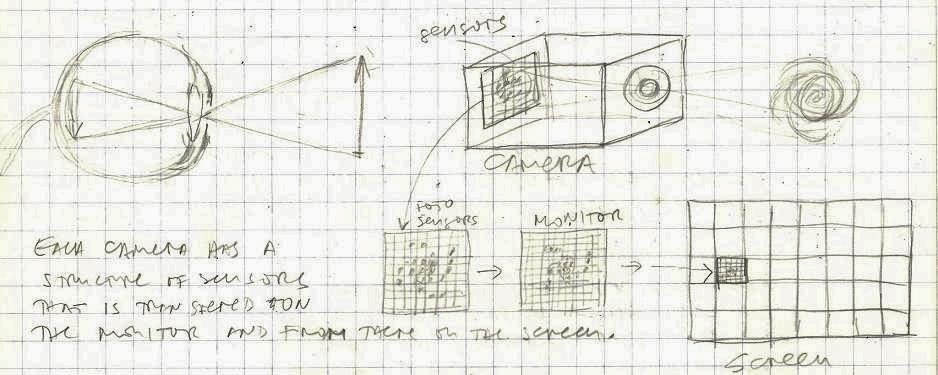
Each camera has a structure of sensors that are transferred to a corresponding monitor and from there to a flat screen. I think that the digital technology today has the possibility to build this kind of system.
A digital camera is almost like an artificial eye. We have a system of lenses and some kind of visual sensors that look like an artificial retina (electronic retina). This electronic retina translates (converts) light waves (photons) into electric signals that became visible again when converted back to light on a digital monitor.
p.38a
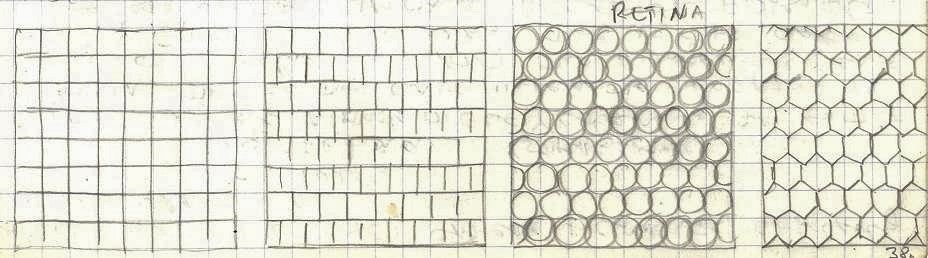
One question is how to organize/define the structure of the “retina” for the standard observer? What would be the structure and the resolution for each individual camera? These are some possibilities.
p.38a1
It seems that the shape of retina and its structure depends on the number of cameras that constitute the inputs for the observer. If there is, for example, only one “camera” that covers the entire sphere then
the retina must be spherical as well.
In these examples, the structure and the resolution of the retinas, the monitors and the screens are provisional (they are illustrations of the ideas). The exact properties of the actual configuration are yet to be determined.
p.39
For the retina, we have to determine:
1. The shape
2. The size
3. The number of sensors
4. The spectrum (wave lengths) it can register
5. The threshold, minimum energy that can be detected
6. The resolution
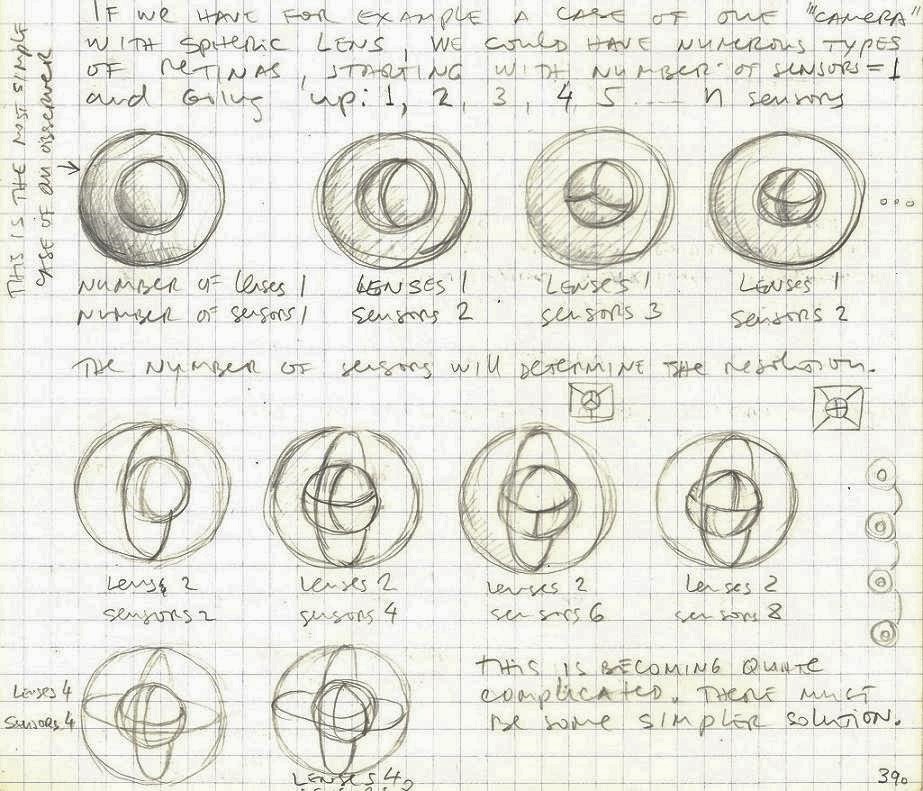
If we have, for example, a case of one “camera” with a spherical lens, we could have numerous types of retinas, starting with the number of sensors: 1, 2, 3,…n.
The number of sensors will determine the resolution. (This is becoming quite complicated. There must be some simpler solution.)
p.39b
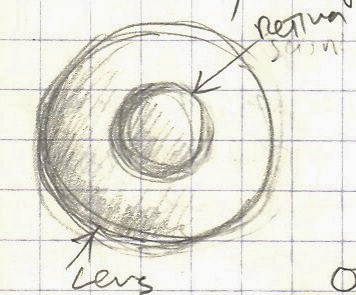
The light receptor (“eye”, “camera”) consists basically of two elements: 1. lens, 2. retina
The lens could be a single (spherical) piece covering the entire (spherical) retina. This is the case when the receptor (“eye”) consists of a single spherical lens and one homogenous (continual) spherical retina. This would be the simplest receptor possible. It has only one lens and the entire retina is one single sensor.
In principle, the retina could consist of one re more light sensors. We assume that if the number of sensors in retina is higher, its resolution is higher as well.
We might consider the outside surface of the lens to be the border between the observer and the observed.
Regarding the sensor (some kind of photo-cell) we would assume that it is homogenous, indivisible, one-piece entity. It is a constitutive unit of the retina. The retina could be a complex structure that consists of many sensors. The minimal size of the observer should correspond to the wave length of the light that this observer can “see” (register).
p.40
While thinking about the size of the observer in relation to the wavelength of the electromagnetic waves it can (is equipped) to register, there are two possibilities:
– To have observers of different sizes that could see em-waves,
– To have one size (standard) observer with different kinds of “lenses” (detectors), convert the non-visible spectrum (radio-waves, gamma-rays), into visible light.
We could construct/build observers that are different in size (macro or micro), or we can use lenses (macro or micro) to simulate a very large or very small observer.
Also, it is a question how many “eyes” (cameras) the standard observer should have, and how many sensors will its retina have, and what would be its structure?
It seems it might be a problem with combining a topological transformation and a resolution. How to present (convert) a coherent system with monitors on one screen?
p.40b
Somehow we will have to assume that there is an infinite grid of squares 1x1cm stretching in all directions (for a 2D space). Also, for a 3D space these will be cubes 1x1x1cm. We’ll consider these to be referential structures, something like the pages of a notebook. This will enable us to determine (define) all other shapes and sizes, in relation to this referential grid.
p.41
There are various ways to transform a cube on a 2D screen. The question of resolution and distortions remains still unresolved.
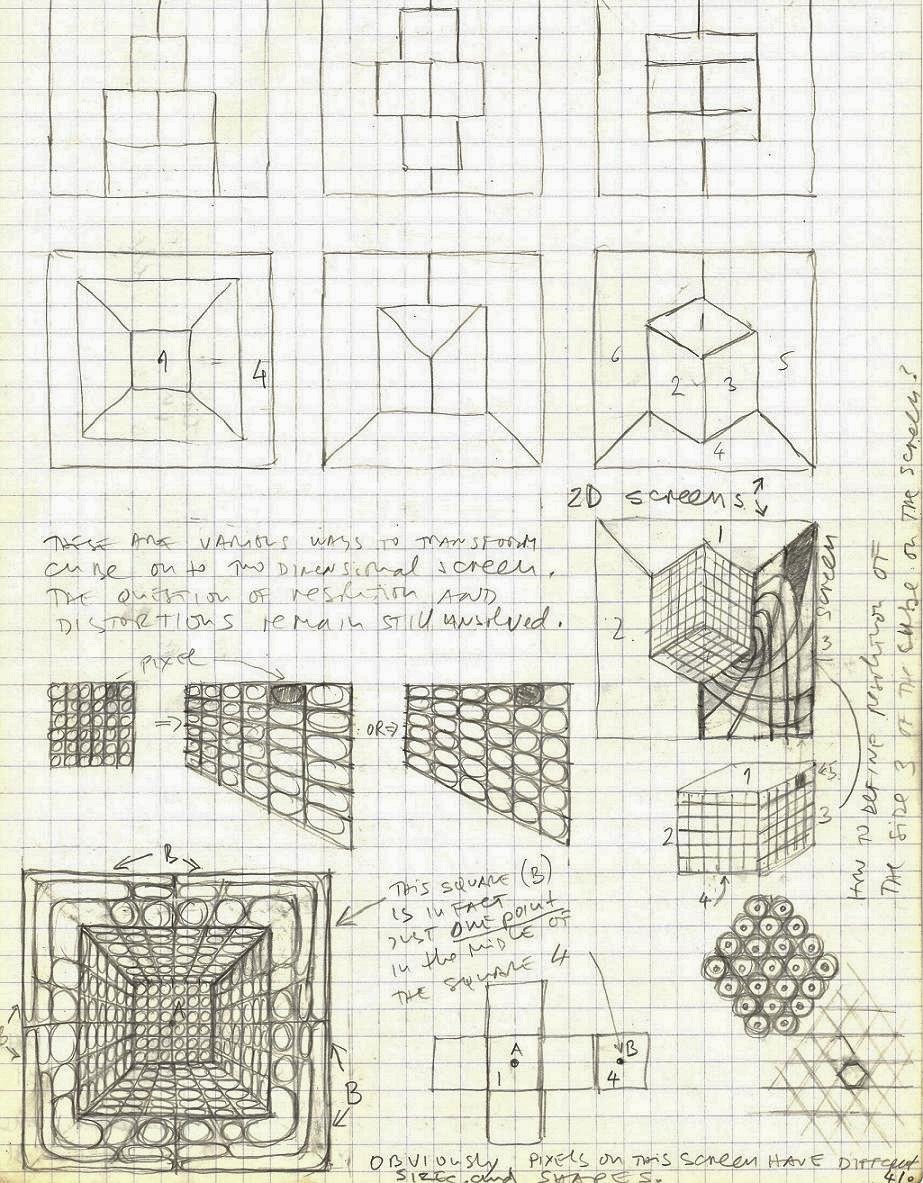
p.41b
Is it possible to imagine a universe in which the “arrow of time” has an opposite direction from ours,
like a film run in reverse? Obviously, in that universe entropy will have the opposite direction as well.
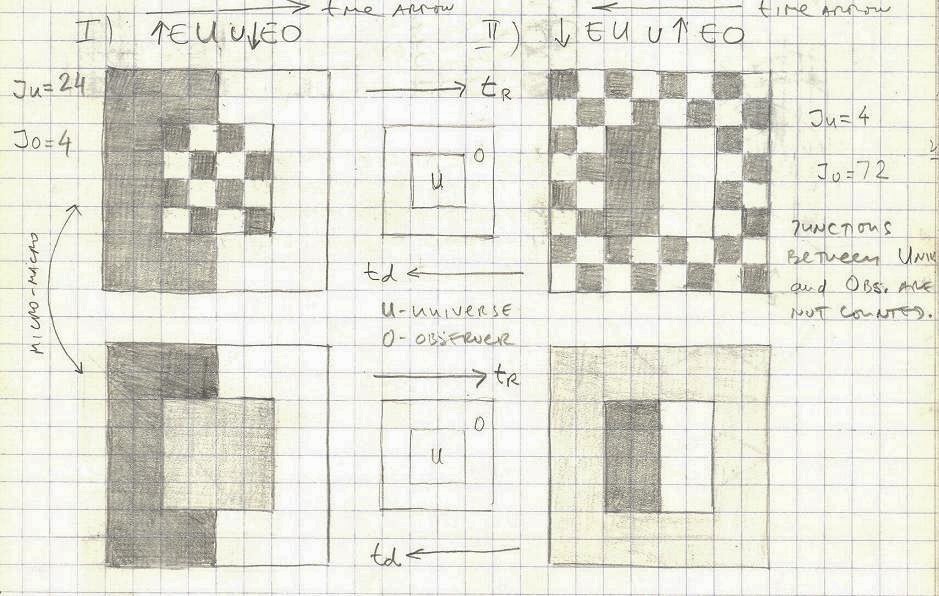
I think the answer is yes. It might be possible to imagine such universe, the only question is how this reflects/effects our process of thinking (remembering)? Is it possible to imagine a process of thinking that follows the negative (reverse) “arrow of time”? Will this kind of observer be losing its memory with time?
p.42
It seems there are two possibilities:
1. if the entropy of the universe is going up, the entropy of the observer is going down. This would be normal (our) arrow of time. In other words, with the passing of time the universe is becoming less organized (entropy goes up) while the observer is becoming more organized (entropy goes down).
2. if the entropy of the universe is going down, the entropy of the observer is going up. This would be a reverse arrow of time. Here, with the revers time flow, the universe is becoming more organized (its entropy goes down) while the observer is becoming less organized (its entropy goes up).

p.42b
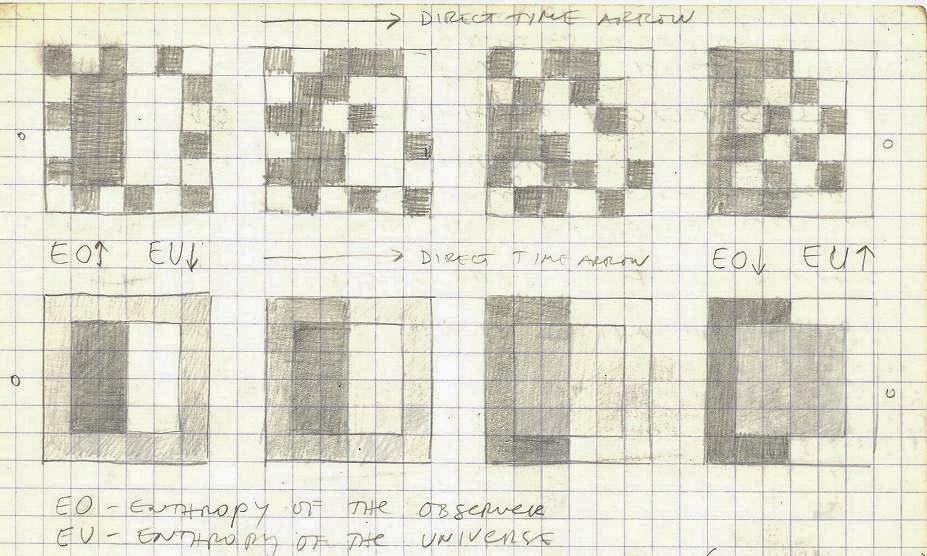
Would it be possible to imagine an observer-universe constellation in which the entropy of both the universe and the observer is going down with time? That both the observer and the universe are becoming more organized with time.
EO – entropy of the observer, EU – entropy of the universe.
We may say that in the universe we experience (direct arrow of time) it seems that that its entropy is going up (becoming less organized), while the entropy of the observer is declining (becoming more organized). And in the reverse time arrow all these processes seems to be in reverse as well.
p.43

p.43a

p.44

This is one possible set of conditions to have a system of a simple observer-universe configuration.
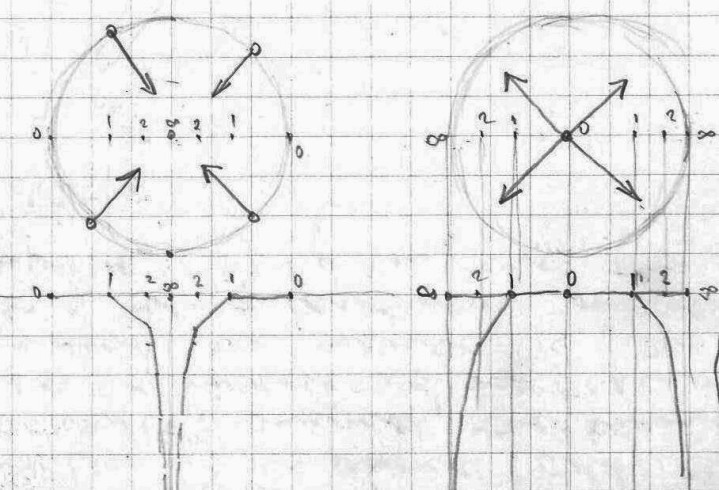
A structure of values (a) consists of three values: black, gray and white, each placed in sets of 16 elements. Here black is the negative of white, while gray is neutral (the negative of gray is gray).
A spatial structure (structure of values) is represented with the 4×4 matrix as shown in the picture (b). In this spatial structure the position of the universe is represented with the four elements in the middle, while the observer is represented with 12 elements around it. Thus in this configuration the observer is on the periphery and surrounding the observed (universe).
p.44

p.45

p.45a

p.46

It seems it is not possible to define any meaningful observer without some kind of memory. Memory would be some kind of saved picture of the universe. This might lead to the conclusion that time and space are properties of the observer(me) projected on the universe.
p.46a

p.47
Why are there two different kinds of change: reversible and irreversible? Or two different concepts of time? Or, are there such differences at all? It may all depend on where the referential point (observer) is and what its properties are.
Everything, any kind of process or change that is recorded by camera (on the film) is reversible. We can always run a film in reverse (backward). When we project a film in reverse, even electrons and photons that are part of the moving body that is recorded, and light (photons) reflected from the body and recorded by the camera, all this should move backwards. And it is only our memory that will inform us (make us aware) that the film is running in reverse.
We can assume that there is no such thing as “change” (time, space, matter, energy, light, etc) in the universe. These are all properties of the observer, defined by the observer, meant for the observer, that are all projected on the world (like “chronology” over time, or Mercator’s grid over the Earth). The universe itself is most likely just “chaos”, or “nothing” (and these two are observer’s notions). What is the continuity (of existence) of the observer? And what would that be without memory? (All this what I am writing here would not be possible without memory.)
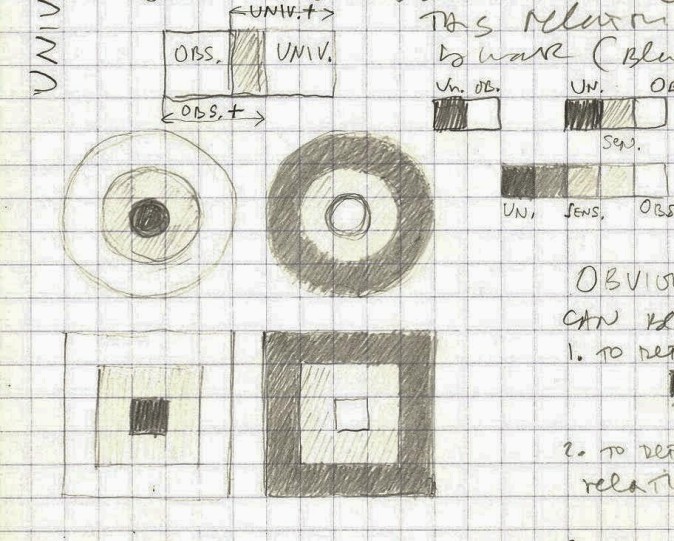
The question is, as I mentioned earlier, where does the observer end and the universe begin? There must be some overlapping (gray) area where the observer and universe meet. The relationship could be either binary (black-white) or threenary (black-gray-white). Gray in fact represents the interface (sensors, screen, membrane, eyes, ears, skin, perhaps even corresponding centers in the brain).
p.50
p.52
In essence, “everything” is “now” and “here”, and these are all human categories. How does the “present” transform (morphs) into the “past”? It probably has something to do with the (anti)entropic characteristics of the observer that relates to the irreversibility of the process of memory.
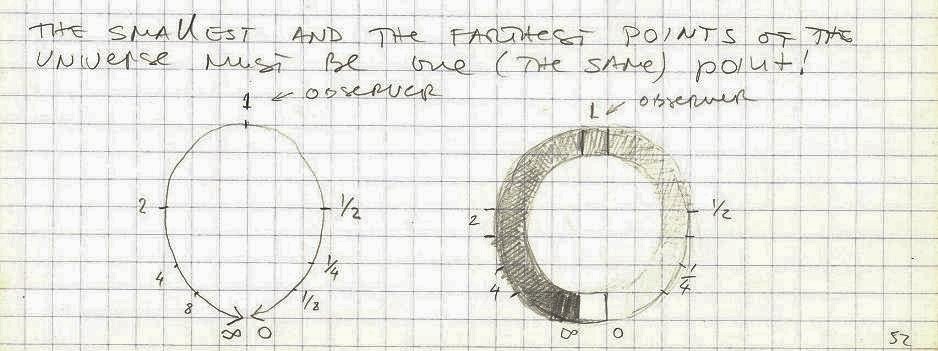
The smallest and the farthest points in the universe are most likely one and the same.
p.53
Operation “negative” could turn infinitely small into infinitely large and finitely small into finitely large, while the observer remains unchanged to this operation (what is the meaning of this?).
Does this mean that all distant objects (galaxies, quasars) are in fact, in some way, just around us?
It is all here but it is so small, much smaller than quarks, that we are not able to see it?
Would it be possible to distinguish (separate) “space” from “matter”? It seems that our notions of magnitude are related more to matter than to space. Let us imagine a sphere of “pure vacuum”, without any traces of matter in it. How would we be able to measure the radius of this sphere with the elements of space that are within it? How would we know if it is
10-10 m or 1010 m? But if we see a proton inside it as the largest object, or in another a galaxy, then we will have the idea of the magnitudes of these two spheres.
Of course, if we, as outside observers, see ourselves to be part of the picture, we could distinguish these two spheres by simply measuring their radius externally. But is there something in the structure of the space itself that could tell us which one is macro and which is a micro space? Is there an intrinsic structure of space itself without any matter (including vacuum)? Is there a specific macro structure of space that is different from its micro-structure? Or, in other words, can we establish a concept of pure macro and micro space without any matter? It is most likely that the micro and macro structures of space are not the same.
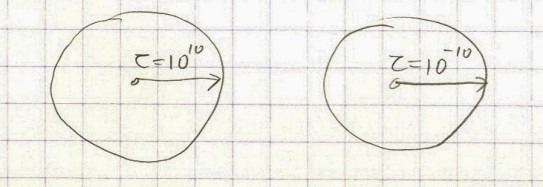
p.54
We could see all this as some kind of a geometry questions. An ideal space (without matter), with the question being what or who is the observer? How to define an observer within an empty geometric space? There are just two scales of orders of magnitude, and not the “structures” of the space.
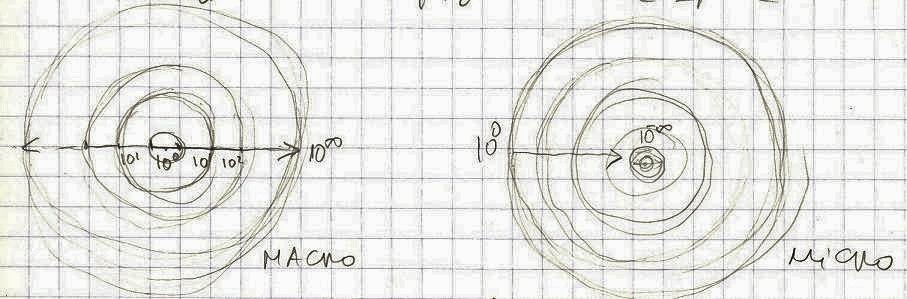
p.54a